题目内容
11.先化简,再求值:(1+$\frac{4}{{a}^{2}-4}$)÷$\frac{a}{a-2}$,其中a=5.分析 原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,把a的值代入计算即可求出值.
解答 解:原式=$\frac{{a}^{2}-4+4}{(a+2)(a-2)}$•$\frac{a-2}{a}$=$\frac{{a}^{2}}{(a+2)(a-2)}$•$\frac{a-2}{a}$=$\frac{a}{a+2}$,
当a=5时,原式=$\frac{5}{7}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
16.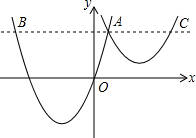 如图,抛物线y1=a(x+2)2-3与y2=$\frac{1}{2}$(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;②a=$\frac{2}{3}$;③当x=0时,y2-y1=6;④AB+AC=10;其中正确结论的个数是( )
如图,抛物线y1=a(x+2)2-3与y2=$\frac{1}{2}$(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;②a=$\frac{2}{3}$;③当x=0时,y2-y1=6;④AB+AC=10;其中正确结论的个数是( )
 如图,抛物线y1=a(x+2)2-3与y2=$\frac{1}{2}$(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;②a=$\frac{2}{3}$;③当x=0时,y2-y1=6;④AB+AC=10;其中正确结论的个数是( )
如图,抛物线y1=a(x+2)2-3与y2=$\frac{1}{2}$(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;②a=$\frac{2}{3}$;③当x=0时,y2-y1=6;④AB+AC=10;其中正确结论的个数是( )| A. | ①②④ | B. | ①③④ | C. | ②③④ | D. | ①②③④ |
3.某中学为筹备校庆,准备印制一批纪念册,每册由4张彩页,6张黑白页构成.印制该纪念册的总费用由制版费和印刷费两部分组成,其中制版费的价格为:彩页300元/张,黑白页50元/张;印刷费用与印数的关系见表:
(1)印制这批纪念册需制版费1500元,印制1千册纪念册的印刷费13000元;
(2)若印制这批纪念册共需y元,则:
①当1≤x<5时,求y关于x的函数表达式;
②当y≤60 080元,最多能印多少册?
| 印数x(千册) | 1≤x<5 | x≥5 |
| 彩色(元/张) | 2.2 | 2.0 |
| 黑白(元/张) | 0.7 | 0.6 |
(2)若印制这批纪念册共需y元,则:
①当1≤x<5时,求y关于x的函数表达式;
②当y≤60 080元,最多能印多少册?
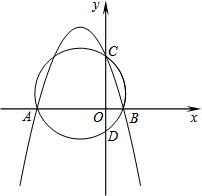 如图,抛物线y=-$\frac{3}{4}$x2-$\frac{9}{4}$x+3与x轴交于点A、B,与y轴交于点C.经过A、B、C三点的圆与y轴的负半轴交于点D.
如图,抛物线y=-$\frac{3}{4}$x2-$\frac{9}{4}$x+3与x轴交于点A、B,与y轴交于点C.经过A、B、C三点的圆与y轴的负半轴交于点D.
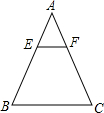 如图,在△ABC中,EF∥BC,$\frac{AE}{EB}$=$\frac{1}{3}$,S四边形BCFE=15,则S△ABC=16.
如图,在△ABC中,EF∥BC,$\frac{AE}{EB}$=$\frac{1}{3}$,S四边形BCFE=15,则S△ABC=16.