题目内容
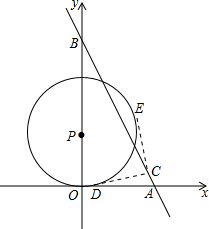 直线l:y=-2x+8与x轴、y轴交于点A、B,点P(0,t)是y轴上一动点,使⊙P的半径为3,在点P运动的过程中,点C是直线上l一点,过点C作⊙P的切线CD、CE,若CD⊥CE,且这样的点C有且只有一个,求C点坐标.
直线l:y=-2x+8与x轴、y轴交于点A、B,点P(0,t)是y轴上一动点,使⊙P的半径为3,在点P运动的过程中,点C是直线上l一点,过点C作⊙P的切线CD、CE,若CD⊥CE,且这样的点C有且只有一个,求C点坐标.考点:圆的综合题
专题:综合题
分析:连接PD、PE、PC,如图1,易证四边形PDCE是正方形,从而求出PC,由于符合条件的点C有且只有一个,因此PC⊥AB,然后分别对点C在y轴的右侧、左侧进行讨论,运用相似三角形的性质就可解决问题.
解答:解:连接PD、PE、PC,如图1.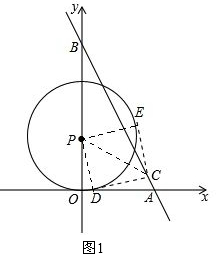
∵CD、CE是⊙P的切线,
∴∠PEC=∠PDC=90°.
∵CD⊥CE,
∴∠DCE=∠PEC=∠PDC=90°,
∴四边形PDCE是矩形.
∵PD=PE,
∴矩形PDCE是正方形.
∴PC=
PD=3
.
∵符合条件的点C有且只有一个,↑
∴PC⊥AB,且PC=3
.
①若点C在y轴的右侧,
过点C作CH⊥OB于H,如图2.
由直线y=-2x+8可知A的坐标为(4,0)、B的坐标为(0,8),
则有OA=4,OB=8,AB=
=4
.
∵∠PBC=∠ABO,∠BCP=∠BOA=90°,
∴△BCP∽△BOA.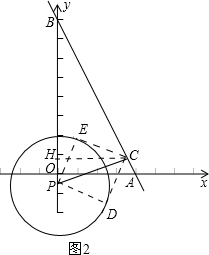
∴
=
=
=
.
∴
=
=
.
∴BC=6
,BP=3
.
同理可得:△BCH∽△BAO.
∴
=
=
.
∴
=
=
.
∴CH=
,BH=
.
∴OH=OB-BH=8-
,
∴点C的坐标为(
,8-
).
②若点C在y轴的左侧,
同理可得:点C的坐标为(-
,8+
).
∴点C的坐标为(
,8-
)或(-
,8+
).

∵CD、CE是⊙P的切线,
∴∠PEC=∠PDC=90°.
∵CD⊥CE,
∴∠DCE=∠PEC=∠PDC=90°,
∴四边形PDCE是矩形.
∵PD=PE,
∴矩形PDCE是正方形.
∴PC=
| 2 |
| 2 |
∵符合条件的点C有且只有一个,↑
∴PC⊥AB,且PC=3
| 2 |
①若点C在y轴的右侧,
过点C作CH⊥OB于H,如图2.
由直线y=-2x+8可知A的坐标为(4,0)、B的坐标为(0,8),
则有OA=4,OB=8,AB=
| 42+82 |
| 5 |
∵∠PBC=∠ABO,∠BCP=∠BOA=90°,
∴△BCP∽△BOA.

∴
| BC |
| BO |
| BP |
| BA |
| CP |
| OA |
3
| ||
| 4 |
∴
| BC |
| 8 |
| BP | ||
4
|
3
| ||
| 4 |
∴BC=6
| 2 |
| 10 |
同理可得:△BCH∽△BAO.
∴
| CH |
| OA |
| BH |
| BO |
| BC |
| BA |
∴
| CH |
| 4 |
| BH |
| 8 |
6
| ||
4
|
∴CH=
6
| ||
| 5 |
12
| ||
| 5 |
∴OH=OB-BH=8-
12
| ||
| 5 |
∴点C的坐标为(
6
| ||
| 5 |
12
| ||
| 5 |
②若点C在y轴的左侧,
同理可得:点C的坐标为(-
6
| ||
| 5 |
12
| ||
| 5 |
∴点C的坐标为(
6
| ||
| 5 |
12
| ||
| 5 |
6
| ||
| 5 |
12
| ||
| 5 |
点评:本题主要考查了切线的性质、正方形的性质、相似三角形的判定与性质、勾股定理等知识,有一定的综合性,需要注意的是点C是动点,它的坐标与位置有关,故需分情况讨论,否则就会出现漏解的现象.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目