题目内容
已知x1、x2是关于x的方程x2+2x+c-3=0的两个实数根,且x1<0<x2,求c的取值范围.
考点:抛物线与x轴的交点
专题:计算题
分析:根据抛物线与x轴的交点问题得到抛物线y=x2+2x+c-3与x轴有两个交点,且与x轴的交点在y轴的两侧,于是得到c-3<0,然后解不等式即可.
解答:解:根据题意抛物线y=x2+2x+c-3与x轴有两个交点,
而x1<0<x2,
所以抛物线y=x2+2x+c-3与x轴的交点在y轴的两侧,
而抛物线开口向下,
所以抛物线与y轴交点在x轴下方,即c-3<0,解得c<3,
所以c的取值范围为c<3.
而x1<0<x2,
所以抛物线y=x2+2x+c-3与x轴的交点在y轴的两侧,
而抛物线开口向下,
所以抛物线与y轴交点在x轴下方,即c-3<0,解得c<3,
所以c的取值范围为c<3.
点评:本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
 已知A,B,C三点作直线AB,射线AC,线段BC.
已知A,B,C三点作直线AB,射线AC,线段BC.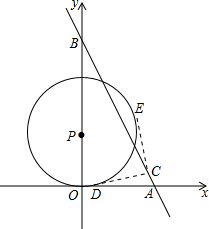 直线l:y=-2x+8与x轴、y轴交于点A、B,点P(0,t)是y轴上一动点,使⊙P的半径为3,在点P运动的过程中,点C是直线上l一点,过点C作⊙P的切线CD、CE,若CD⊥CE,且这样的点C有且只有一个,求C点坐标.
直线l:y=-2x+8与x轴、y轴交于点A、B,点P(0,t)是y轴上一动点,使⊙P的半径为3,在点P运动的过程中,点C是直线上l一点,过点C作⊙P的切线CD、CE,若CD⊥CE,且这样的点C有且只有一个,求C点坐标. 如图,已知线段AB=12cm,点C为AB上的一个动点,点D、E分别是AC和BC的中点.
如图,已知线段AB=12cm,点C为AB上的一个动点,点D、E分别是AC和BC的中点.