题目内容
12.已知点P是第二象限角平分线上的一点,且点P到原点的距离为4,那么点P的坐标为(-2$\sqrt{2}$,2$\sqrt{2}$).分析 根据第二象限角平分线上的点的坐标特征,设P(t,-t)(t<0),根据两点间的距离公式得到t2+(-t)2=42,然后解方程求出t即可得到P点坐标.
解答 解:∵P是直角坐标系第二象限角平分线上的点,
∴点P的横纵坐标的绝对值相等,
设P(t,-t)(t<0),
∵P到原点的距离是4,
∴t2+(-t)2=42,解得t1=-2$\sqrt{2}$,t2=2$\sqrt{2}$(舍去),
∴P点坐标为(-2$\sqrt{2}$,2$\sqrt{2}$).
故答案为:(-2$\sqrt{2}$,2$\sqrt{2}$).
点评 本题考查了点的坐标,与图形的现在,坐标平面内的点与有序实数对是一一对应的关系;记住各象限和坐标轴上点的坐标特征.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
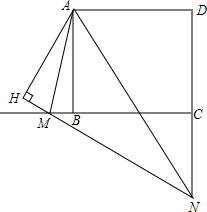 已知:如图,在正方形ABCD中,M在CB延长线上,N在DC延长线上,∠MAN=45°,AH⊥MN,垂足为H,求证:
已知:如图,在正方形ABCD中,M在CB延长线上,N在DC延长线上,∠MAN=45°,AH⊥MN,垂足为H,求证: 如图,E是平行四边形ABCD边AD上一点,且AE:ED=1:2,CE与BD交于点O,则BO:OD=3:2.
如图,E是平行四边形ABCD边AD上一点,且AE:ED=1:2,CE与BD交于点O,则BO:OD=3:2.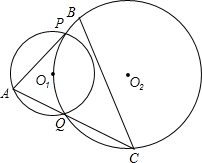 如图,⊙O1与⊙O2交于P、Q两点,且⊙O2经过点O1,A是⊙O1的优弧$\widehat{PQ}$上任一点,AP、AQ的延长线与⊙O2分别交于点B、C.证明:O1为△ABC的垂心.
如图,⊙O1与⊙O2交于P、Q两点,且⊙O2经过点O1,A是⊙O1的优弧$\widehat{PQ}$上任一点,AP、AQ的延长线与⊙O2分别交于点B、C.证明:O1为△ABC的垂心. 如图,A、P、B、C四点都在⊙O上,且∠1=∠2=60°,判断△ABC的形状并证明你的结论.
如图,A、P、B、C四点都在⊙O上,且∠1=∠2=60°,判断△ABC的形状并证明你的结论.