题目内容
3.Rt△ABC中,∠C=90°,∠B=30°,BC=4cm,⊙C的半径为2.5cm,则⊙C与直线的位置关系是( )| A. | 相切 | B. | 相离 | C. | 相交 | D. | 相切或相交 |
分析 过C作CD⊥AB于D,由含30°角的直角三角形的性质求出CD,得出d<r,根据直线和圆的位置关系即可得出结论.
解答 解:过C作CD⊥AB于D,如图所示:
则∠CDB=90°,
∵∠B=30°,BC=4cm,
∴CD=$\frac{1}{2}$BC=2cm,
∵⊙C的半径为2.5cm,
∴d<r,
∴⊙C与直线AB的关系是相交,
故选:C.
点评 本题考查了直线和圆的位置关系、含30°角的直角三角形的性质;解此题的关键是能正确作出辅助线,求出CD的长,注意:直线和圆的位置关系有:相离,相切,相交.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.若点A(m,2)与点B(3,n)关于x轴对称,则m+n的值是( )
| A. | 1 | B. | -2 | C. | 2 | D. | 5 |
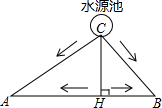 如图所示,A、B两块试验田相距200米,C为水源地,AC=160m,BC=120m,为了方便灌溉,现有两种方案修筑水渠.
如图所示,A、B两块试验田相距200米,C为水源地,AC=160m,BC=120m,为了方便灌溉,现有两种方案修筑水渠.