题目内容
11.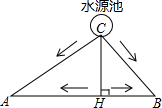 如图所示,A、B两块试验田相距200米,C为水源地,AC=160m,BC=120m,为了方便灌溉,现有两种方案修筑水渠.
如图所示,A、B两块试验田相距200米,C为水源地,AC=160m,BC=120m,为了方便灌溉,现有两种方案修筑水渠.甲方案:从水源地C直接修筑两条水渠分别到A、B;
乙方案;过点C作AB的垂线,垂足为H,先从水源地C修筑一条水渠到AB所在直线上的H处,再从H分别向A、B进行修筑.
(1)请判断△ABC的形状(要求写出推理过程);
(2)两种方案中,哪一种方案所修的水渠较短?请通过计算说明.
分析 (1)由勾股定理的逆定理即可得出△ABC是直角三角形;
(2)由△ABC的面积求出CH,得出AC+BC<CH+AH+BH,即可得出结果.
解答 解:(1)△ABC是直角三角形;理由如下:
∴AC2+BC2=1602+1202=40000,AB2=2002=40000,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°;
(2)甲方案所修的水渠较短;理由如下:
∵△ABC是直角三角形,
∴△ABC的面积=$\frac{1}{2}$AB•CH=$\frac{1}{2}$AC•BC,
∴CH=$\frac{AC•BC}{AB}$=$\frac{160×120}{200}$=96(m),
∵CH⊥AB,
∴∠AHC=90°,
∴AH=$\sqrt{A{C}^{2}-C{H}^{2}}$=$\sqrt{16{0}^{2}-9{6}^{2}}$=128(m),
∴BH=AB-AH=72m,
∵AC+BC=160m+120m=280m,CH+AH+BH=96m+200m=296m,
∴AC+BC<CH+AH+BH,
∴甲方案所修的水渠较短.
点评 本题考查了勾股定理的应用、勾股定理的逆定理、三角形面积的计算;熟练掌握勾股定理,由勾股定理的逆定理证出△ABC是直角三角形是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知x=-2是方程x2-4x+c=0的一个根,则c的值是( )
| A. | -12 | B. | -4 | C. | 4 | D. | 12 |
3.Rt△ABC中,∠C=90°,∠B=30°,BC=4cm,⊙C的半径为2.5cm,则⊙C与直线的位置关系是( )
| A. | 相切 | B. | 相离 | C. | 相交 | D. | 相切或相交 |
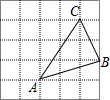 如图,每个小方格都是边长为1个单位的小正方形,A,B,C三点都是格点(每个小方格的顶点叫格点).
如图,每个小方格都是边长为1个单位的小正方形,A,B,C三点都是格点(每个小方格的顶点叫格点). 如图,若DE∥BC,且AD=4cm,DB=2cm,AC=9cm,则AE=6cm.
如图,若DE∥BC,且AD=4cm,DB=2cm,AC=9cm,则AE=6cm.