题目内容
14.先化简,再求值:(a2-4)($\frac{a}{a+2}$-$\frac{1}{a-2}$-1),其中a=-3.分析 先把(a2-4)分解因式,再利用乘法的分配律进行计算得到原式=a(a-2)-(a+2)-(a+2)(a-2),接着去括号合并即可得到原式=-3a+2,然后把a=-3代入计算即可.
解答 解:原式=(a+2)(a-2)•($\frac{a}{a+2}$-$\frac{1}{a-2}$-1),
=a(a-2)-(a+2)-(a+2)(a-2)
=a2-2a-a-2-a2+4
=-3a+2,
当a=-3时,原式=-3×(-3)+2=11.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.若x>y,则下列不等式成立的是( )
| A. | x-3<y-3 | B. | x+5>y+5 | C. | $\frac{x}{3}$<$\frac{y}{3}$ | D. | -2x>-2y |
5.点M(2,1)关于x轴对称的点的坐标是( )
| A. | (1,-2) | B. | (-2,1) | C. | (2,-1) | D. | (-1,2) |
3.Rt△ABC中,∠C=90°,∠B=30°,BC=4cm,⊙C的半径为2.5cm,则⊙C与直线的位置关系是( )
| A. | 相切 | B. | 相离 | C. | 相交 | D. | 相切或相交 |
4.如图,有四个大小相同的小长方形和两个大小相同的大长方形按如图位置摆放,按照图中所示尺寸,则小长方形的长与宽的差是( )
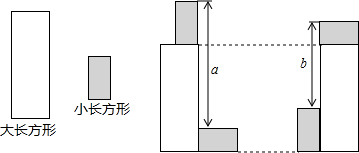

| A. | 3b-2a | B. | $\frac{a-b}{2}$ | C. | $\frac{a-b}{3}$ | D. | $\frac{a}{3}-\frac{b}{4}$ |
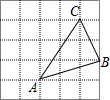 如图,每个小方格都是边长为1个单位的小正方形,A,B,C三点都是格点(每个小方格的顶点叫格点).
如图,每个小方格都是边长为1个单位的小正方形,A,B,C三点都是格点(每个小方格的顶点叫格点).