题目内容
1．若二次函数y=ax2+bx+c（a≠0）中x与y的对应值如表：| x | -7 | -6 | -5 | -4 | -3 | -2 |
| y | -27 | -13 | -3 | 3 | 5 | 3 |
| A． | 5 | B． | -3 | C． | -13 | D． | -27 |
分析 利用二次函数的对称性得出对称轴以及x=-2与x=-4时对应y的值相等，x=1与x=-7时对应y的值相等，即可得出答案．
解答 解：根据图表得出：当x=-2，-4时，对应y的值为3，故此函数的对称轴为x=-3，
则利用二次函数的对称性得出x=1与x=-7时对应y的值相等，
故当x=1时，y的值为-27，
故选D．
点评 此题主要考查了二次函数的性质，利用二次函数对称性得出x=0与x=-6时对应y的值相等是解题关键．
练习册系列答案
智能训练练测考系列答案
相关题目
10．每年的天猫双十一购物狂欢节是中国的“剁手节”，也是马云最赚钱的一天，2016年阿里天猫双十一狂欢节中成交额突破1200亿，120000000000用科学记数法表示为（ ）
| A． | 1.2×1010 | B． | 12×109 | C． | 0.12×1011 | D． | 1.2×1011 |
12．已知正方形ABCD的边长为1，E、F分别为BC、CD上的点，且满足BE=CF，则△AEF的面积的最小值是（ ）
| A． | $\frac{\sqrt{2}}{8}$ | B． | $\frac{\sqrt{3}}{8}$ | C． | $\frac{1}{4}$ | D． | $\frac{3}{8}$ |
如图，四边形ABCD中，对角线AC⊥BD于点O，且AO=BO=4，CO=8，∠ADB=2∠ACB，则四边形ABCD的面积为42．
6．
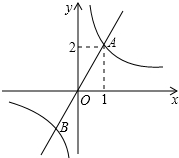如图，函数y1=$\frac{{k}_{1}}{x}$与y2=k2x的图象相交于点A（1，2）和点B，当y1＜y2时，自变量x的取值范围是（ ）
如图，函数y1=$\frac{{k}_{1}}{x}$与y2=k2x的图象相交于点A（1，2）和点B，当y1＜y2时，自变量x的取值范围是（ ）| A． | x＞l | B． | -1＜x＜0 | C． | -l＜x＜0 或x＞l | D． | x＜-1 或 0＜x＜1 |
如图：小敏做了一个角平分仪ABCD，其中AB=AD，BC=DC，将仪器上的点A与∠PRQ的顶点R重合，调整AB与AD，使他们分别落在角的两边上，过点A、C画一条射线AE，AE就是∠PRQ的平分线．试利用全等知识，说明角平分仪的画图原理．