题目内容
5.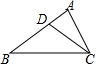 如图,点D是△ABC的AB边上一点,且AB=6,BD=4,AC=2$\sqrt{3}$.
如图,点D是△ABC的AB边上一点,且AB=6,BD=4,AC=2$\sqrt{3}$.(1)求证:△ACD∽△ABC.
(2)若BC=9,求CD的值.
分析 (1)由$\frac{AD}{AC}$=$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$、$\frac{AC}{AB}$=$\frac{2\sqrt{3}}{6}$=$\frac{\sqrt{3}}{3}$知$\frac{AD}{AC}$=$\frac{AC}{AB}$,结合∠A=∠A可得;
(2)由△ACD∽△ABC知$\frac{CD}{BC}$=$\frac{AC}{AB}$,即$\frac{CD}{9}$=$\frac{2\sqrt{3}}{6}$,解之可得.
解答 解:(1)∵AB=6,BD=4,AC=2$\sqrt{3}$,
∴AD=AB-BD=6-4=2,
∴$\frac{AD}{AC}$=$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,$\frac{AC}{AB}$=$\frac{2\sqrt{3}}{6}$=$\frac{\sqrt{3}}{3}$,
则$\frac{AD}{AC}$=$\frac{AC}{AB}$,
∵∠A=∠A,
∴△ACD∽△ABC;
(2)∵△ACD∽△ABC,
∴$\frac{CD}{BC}$=$\frac{AC}{AB}$,即$\frac{CD}{9}$=$\frac{2\sqrt{3}}{6}$,
解得:CD=3$\sqrt{3}$.
点评 本题主要考查相似三角形的判定与性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
20.下列运算正确的是( )
| A. | -22=4 | B. | (3$\frac{1}{2}$)3=-8$\frac{1}{27}$ | C. | (-$\frac{1}{2}$)3=-$\frac{1}{8}$ | D. | (-2)3=-6 |
16.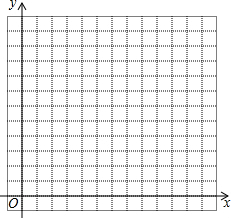 设△ABC中BC边的长为x(cm),BC上的高线AD为y(cm),现一探究小组测得两个变量x(x>0),y(y>0)的一组对应值如表:
设△ABC中BC边的长为x(cm),BC上的高线AD为y(cm),现一探究小组测得两个变量x(x>0),y(y>0)的一组对应值如表:
(1)在如图的坐标系中,用描点法画出相应函数的图线;
(2)求y关于x的函数解析式;
(3)如果三角形BC边的长不小于8cm,求高线AD范围.
 设△ABC中BC边的长为x(cm),BC上的高线AD为y(cm),现一探究小组测得两个变量x(x>0),y(y>0)的一组对应值如表:
设△ABC中BC边的长为x(cm),BC上的高线AD为y(cm),现一探究小组测得两个变量x(x>0),y(y>0)的一组对应值如表:| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 6 | 2.9 | 2.1 | 1.5 | 1.2 | 1 |
(2)求y关于x的函数解析式;
(3)如果三角形BC边的长不小于8cm,求高线AD范围.
10.下列图形中,能够折叠成正方体的是( )
| A. |  | B. |  | C. |  | D. |  |
14. 如图,已知AB∥DE,∠C=30°,∠CDE=140°,则∠ABC的值为( )
如图,已知AB∥DE,∠C=30°,∠CDE=140°,则∠ABC的值为( )
 如图,已知AB∥DE,∠C=30°,∠CDE=140°,则∠ABC的值为( )
如图,已知AB∥DE,∠C=30°,∠CDE=140°,则∠ABC的值为( )| A. | 20° | B. | 30° | C. | 40° | D. | 70° |
15.等腰三角形的一个角是80°,则它的底角是( )
| A. | 50° | B. | 80° | C. | 20°或80° | D. | 50°或80° |