题目内容
将抛物线y=ax2﹣1平移后与抛物线y=a（x﹣1）2重合，抛物线y=ax2﹣1上的点A（2，3）同时平移到A′，那么点A′的坐标为（ ）
A. （3，4） B. （1，2） C. （3，2） D. （1，4）
A
【解析】【解析】
∵抛物线y=ax2﹣1的顶点坐标是（0，﹣1），抛物线y=a（x﹣1）2的顶点坐标是（1，0），∴将抛物线y=ax2﹣1向右平移1个单位，再向上平移1个单位得到抛物线y=a（x﹣1）2，∴将点A（2，3）向右平移1个单位，再向上平移1个单位得到点A′的坐标为（3，4）．
故选A．
如图，等边△ABC的边长是2，D、E分别为AB、AC的中点，延长BC至点F，使CF=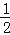
BC，连接CD和EF．
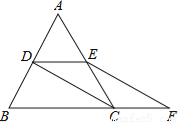
（1）求证：DE=CF；
（2）求EF的长．
见解析；
【解析】试题分析：（1）直接利用三角形中位线定理得出DEBC，进而得出DE=FC；
（2）利用平行四边形的判定与性质得出DC=EF，进而利用等边三角形的性质以及勾股定理得出EF的长
试题解析：（1）证明：∵D、E分别为AB、AC的中点， ∴DEBC，
∵延长BC至点F，使CF=BC， ∴DEFC， 即DE=CF；
（2）【解析】
∵DEFC， ∴四边形DE... 如图，在△ABC中，∠ABC=90°，AB=8，BC=6．若DE是△ABC的中位线，延长DE交△ABC的外角∠ACM的平分线于点F，则线段DF的长为（ ）
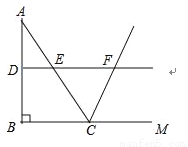
A. 7 B. 8 C. 9 D. 10
B
【解析】试题分析：在RT△ABC中，∵∠ABC=90°，AB=8，BC=6，∴AC===10，∵DE是△ABC的中位线，∴DF∥BM，DE=BC=3，∴∠EFC=∠FCM，∵∠FCE=∠FCM，∴∠EFC=∠ECF，∴EC=EF=AC=5，∴DF=DE+EF=3+5=8．故选B． 在平面直角坐标系xOy中，抛物线y=ax2+bx+2过B（﹣2，6），C（2，2）两点．
（1）记抛物线顶点为D，求△BCD的面积；
（2）若直线y=﹣
x向上平移b个单位所得的直线与抛物线段BDC（包括端点B、C）部分有两个交点，求b的取值范围．
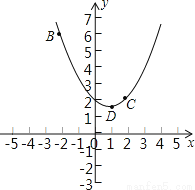
（1）3 （2）＜b≤3．
【解析】（1）根据待定系数法即可解决问题．求出直线BC与对称轴的交点H，根据S△BDC=S△BDH+S△DHC即可解决问题．
（2）由，当方程组只有一组解时求出b的值，当直线y=﹣x+b经过点C时，求出b的值，当直线y=﹣x+b经过点B时，求出b的值，由此即可解决问题．
【解析】
（1）由题意解得，
∴抛物线解析式为y=x2﹣x+2．
∵... 抛物线y=﹣x2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表所示：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知，下列说法中，错误的是（ ）
A. 抛物线与x轴的一个交点坐标为（﹣2，0） B. 抛物线与y轴的交点坐标为（0，6）
C. 抛物线的对称轴是直线x=0 D. 抛物线在对称轴左侧部分是上升的
C
【解析】【解析】
当x=﹣2时，y=0，∴抛物线过（﹣2，0），∴抛物线与x轴的一个交点坐标为（﹣2，0），故A正确；
当x=0时，y=6，∴抛物线与y轴的交点坐标为（0，6），故B正确；
当x=0和x=1时，y=6，∴对称轴为x=，故C错误；
当x＜时，y随x的增大而增大，∴抛物线在对称轴左侧部分是上升的，故D正确；
故选C． 如图，小河上有一拱桥，拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE、ED、DB组成，已知河底ED是水平的，ED＝16m，AE＝8m，抛物线的顶点C到ED的距离是11m，以ED所在的直线为x轴，抛物线的对称轴为y轴建立平面直角坐标系．
(1)求抛物线的解析式；
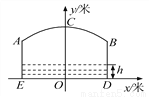
(2)已知从某时刻开始的40h内，水面与河底ED的距离h(单位：m)随时间t(单位：h)的变化满足函数关系h＝－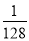
(t－19)2＋8(0≤t≤40)且当水面到顶点C的距离不大于5m时，需禁止船只通行，请通过计算说明：在这一时段内，需多少小时禁止船只通行？
(1)y＝－x2＋11(2)禁止船只通行时间为32小时．
【解析】二次函数的应用，待定系数法，曲线上点的坐标与方程的关系。
（1）根据抛物线特点设出二次函数解析式，把B坐标代入即可求解。
（2）水面到顶点C的距离不大于5米时，即水面与河底ED的距离h至多为6，把6代入所给二次函数关系式，求得t的值，相减即可得到禁止船只通行的时间。 二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论：
⑴ac＜0；
⑵当x＞1时，y的值随x值的增大而减小．
⑶3是方程ax2+（b﹣1）x+c=0的一个根；
⑷当﹣1＜x＜3时，ax2+（b﹣1）x+c＞0．
其中正确的个数为（ ）
A. 4个 B. 3个 C. 2个 D. 1个
B
【解析】二次函数过（-1，-1），（0,3），（1,5），
，
解得,y=-.对称轴,,
(1)正确，（2）开口向下，对称轴，x＞1时y先增大再减小,错误，（3）+2,解得， .正确，（4）+2,所以由（3）得到函数与x轴的交点，作图知，﹣1＜x＜3时,y>0正确.
所以（1）（3）（4）正确.选B. 下列事件中，是必然事件的是（ ）
A. 打开电视机，里面正在转播足球比赛 B. 小麦的亩产量一定为1000公斤
C. 在只装有5个红球的袋中摸出1球是红球 D. 在农历十五的晚上，一定能看到圆月
C
【解析】选项A，B，D选项为不确定事件，即随机事件；选项C是必然发生事件．故选C． 如图，若△DEF是由△ABC经过平移后得到的，则平移的距离是（ ）
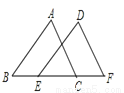
A. 线段BC的长度 B. 线段BE的长度 C. 线段EC的长度 D. 线段EF的长度
B
【解析】试题分析：对应点之间的距离就是平移的距离，根据题意可得：点B和点E对应，则线段BE的长度就是平移的距离.