题目内容
菱形ABCD的对角线AC,BD相交于点O,AC=16,BD=12,以O为圆心作圆与AB相切,则这个圆的直径长为 .
考点:菱形的性质,切线的性质
专题:
分析:首先利用菱形的性质得出AO=CO=8,BO=DO=6,AC⊥BD,再利用勾股定理得出AB的长,结合三角形面积求出即可.
解答: 解:如图所示:∵菱形ABCD的对角线AC,BD相交于点O,AC=16,BD=12,
解:如图所示:∵菱形ABCD的对角线AC,BD相交于点O,AC=16,BD=12,
∴AO=CO=8,BO=DO=6,AC⊥BD,
∴AB=10,
∵EO×AB=AO×BO,
则EO=
=
=4.8,
故以O为圆心作圆与AB相切,则这个圆的直径长为:9.6.
故答案为:9.6.
 解:如图所示:∵菱形ABCD的对角线AC,BD相交于点O,AC=16,BD=12,
解:如图所示:∵菱形ABCD的对角线AC,BD相交于点O,AC=16,BD=12,∴AO=CO=8,BO=DO=6,AC⊥BD,
∴AB=10,
∵EO×AB=AO×BO,
则EO=
| AO×BO |
| AB |
| 8×6 |
| 10 |
故以O为圆心作圆与AB相切,则这个圆的直径长为:9.6.
故答案为:9.6.
点评:此题主要考查了菱形的性质以及切线的性质,利用三角形面积求出是解题关键.

练习册系列答案
相关题目
当-2≤x≤1时,二次函数y=-(x-m)2+m2+1有最大值4,则实数m的值为( )
A、-
| ||||
B、
| ||||
C、2或-
| ||||
D、2或
|
在抛物线y=-x2+2x-3中,若y随x的增大而增大,则x的取值范围是( )
| A、0<x<1 | B、x<1 |
| C、x>1 | D、x>-1 |
一批学生列队从学校到甲地去春游,他们以每小时4千米的速度行进,走了1千米路时,一学生奉命回校取物,他以每小时5千米的速度回校取物后即以同样速度追赶队伍,结果同时到达甲地,求学校到甲地距离是多少?设学校到甲地距离为x千米,则可列出方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
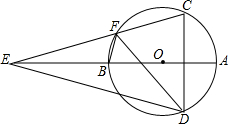 如图,⊙O中,弦CD⊥直径AB,E为AB延长线上一点,CE交⊙O于F.若DF=EF.求证:FB⊥DE.
如图,⊙O中,弦CD⊥直径AB,E为AB延长线上一点,CE交⊙O于F.若DF=EF.求证:FB⊥DE.