题目内容
已知一直线上有A、B、C三点,且线段AB=5,线段AC=2,D为线段BC上一点,且BD=
BC,则CD的长为 .
| 1 |
| 3 |
考点:两点间的距离
专题:
分析:分C在线段AB上和在线段BA的延长线上,可先求得BC,再求得BD,结合条件可求得CD.
解答:解:当点C在线段AB上时,如图1:

∵AB=5,AC=2,
∴BC=AB-AC=5-2=3,
∴BD=
BC=1,
∴CD=BC-BD=3-1-2;
当点C在线段BA的延长线上时,如图2:

∵AB=5,AC=2,
∴BC=AB+AC=2+5=7,
∴BD=
BC=
,
∴CD=BC-BD=7-
=
.
故答案为:2或
.

∵AB=5,AC=2,
∴BC=AB-AC=5-2=3,
∴BD=
| 1 |
| 3 |
∴CD=BC-BD=3-1-2;
当点C在线段BA的延长线上时,如图2:

∵AB=5,AC=2,
∴BC=AB+AC=2+5=7,
∴BD=
| 1 |
| 3 |
| 7 |
| 3 |
∴CD=BC-BD=7-
| 7 |
| 3 |
| 14 |
| 3 |
故答案为:2或
| 14 |
| 3 |
点评:本题主要考查线段长度的计算,确定出点C的位置是解题的关键,注意分类讨论思想的应用.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
无论a,b为何值,代数式a2+b2+4b+5-2a的值总是( )
| A、非负数 | B、0 | C、正数 | D、负数 |
 C为等腰△ABE一腰AB延长线上一点且BC=EF,C,D,F三点共线,求证:CD=DF.
C为等腰△ABE一腰AB延长线上一点且BC=EF,C,D,F三点共线,求证:CD=DF.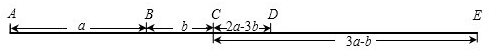
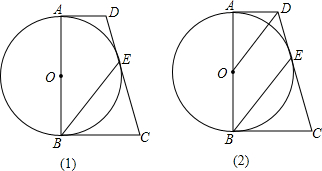
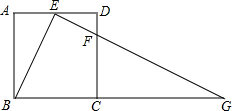 如图,在正方形ABCD中,E,F分别是边AD,CD上的点,AE=ED,DF=
如图,在正方形ABCD中,E,F分别是边AD,CD上的点,AE=ED,DF=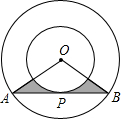 如图,两同心圆的圆心为O,半径分别为6,3,大圆的弦AB切小圆于P,则图中阴影部分的周长是
如图,两同心圆的圆心为O,半径分别为6,3,大圆的弦AB切小圆于P,则图中阴影部分的周长是