题目内容
2.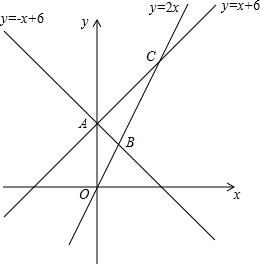 如图,直线y=-x+6交直线y=x+6于点A,直线y=-x+6与直线y=2x相交于点B,直线y=x+6与直线y=2x相交于点C.
如图,直线y=-x+6交直线y=x+6于点A,直线y=-x+6与直线y=2x相交于点B,直线y=x+6与直线y=2x相交于点C.(1)求点B的坐标;
(2)求三角形ABC的面积;
(3)若点P是直线y=2x上的动点,当△ABP的面积等于△AOC的面积时,求点P的坐标.
分析 (1)通过解方程组$\left\{\begin{array}{l}{y=-x+6}\\{y=2x}\end{array}\right.$确定B点坐标;
(2)先求出A、C两点的坐标,然后根据S△ABC=S△AOC-S△AOB,利用三角形面积公式计算即可求解;
(3)分点P在第一象限与第三象限两种情况进行讨论.
解答 解:(1)解方程组$\left\{\begin{array}{l}{y=-x+6}\\{y=2x}\end{array}\right.$,得$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$,
所以B点坐标为(2,4);
(2)将y=-x+6代入y=x+6,
得-x+6=x+6,
解得x=0,
则y=6,
所以A点坐标为(0,6);
将y=x+6代入y=2x,
得x+6=2x,
解得x=6,
则y=12,
所以C点坐标为(6,12);
S△ABC=S△AOC-S△AOB
=$\frac{1}{2}$×6×6-$\frac{1}{2}$×6×2
=18-6=12;
(3)点P是直线y=2x上的动点,设P(a,2a).分两种情况: ①如果点P在第一象限,
①如果点P在第一象限,
∵S△ABP=S△AOP-S△AOB
=$\frac{1}{2}$×6×a-$\frac{1}{2}$×6×2
=3a-6,
∴当△ABP的面积等于△AOC的面积时,有3a-6=18,
解得a=8,
∴点P的坐标为(8,16);
②如果点P在第三象限,
∵S△ABP=S△AOP+S△AOB
=$\frac{1}{2}$×6×(-a)+$\frac{1}{2}$×6×2
=-3a+6,
∴当△ABP的面积等于△AOC的面积时,有-3a+6=18,
解得a=-4,
∴点P的坐标为(-4,-8);
综上所述,点P的坐标为(8,16)或(-4,-8).
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解.也考查了三角形面积公式.

| A. | $\sqrt{16}$=±4 | B. | $\root{3}{8}$=±2 | C. | (-$\sqrt{2}$)4=-4 | D. | ($\root{5}{-8}$)5=-8 |
| A. | -$\frac{2}{5}$是$\sqrt{\frac{4}{25}}$的平方根 | B. | -$\frac{2}{5}$是$\frac{4}{25}$的平方根 | ||
| C. | $\frac{4}{25}$的平方根是-$\frac{2}{5}$ | D. | $\sqrt{\frac{4}{25}}$的平方根是±$\frac{2}{5}$ |
| A. | 该方程一定是一元二次方程 | B. | 当k>1时,此方程一定有实数根 | ||
| C. | 当k<1时,此方程可能没有实数根 | D. | 当k<0时,此方程一定有实数根 |
 如图,AC是⊙O的直径,点B在⊙O上,∠BAC=60°
如图,AC是⊙O的直径,点B在⊙O上,∠BAC=60°


