题目内容
13.是否存在这样的整数x,使它同时满足下列两个条件:(1)式子$\sqrt{x-13}$和$\sqrt{20-x}$都有意义;(2)$\sqrt{x}$仍是整数?如果存在,求出来,如果不存在,请说明理由.分析 首先根据二次根式有意义的条件可得:$\left\{\begin{array}{l}{x-13≥0}\\{20-x≥0}\end{array}\right.$,解不等式组可得13≤x≤20,然后再根据$\sqrt{20}$的值是整数可确定x=16.
解答 解:存在,
由式子$\sqrt{x-13}$和$\sqrt{20-x}$都有意义,
可得:$\left\{\begin{array}{l}{x-13≥0}\\{20-x≥0}\end{array}\right.$,
解得:13≤x≤20,
又∵$\sqrt{x}$仍是整数,
∴x=16
点评 此题主要考查了二次根式有意义的条件,关键是掌握二次根式中的被开方数是非负数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.若方程3m(x+1)+1=m(3-x)-5x的解是小于1的正数,则m的取值范围是( )
| A. | m>-1.5 | B. | m<-1.5 | C. | m>1.5 | D. | m<1.5 |
4.下列说法正确的是( )
| A. | 两个有理数的和不小于每个加数 | |
| B. | 互为相反数的两个数,它们的平方相同 | |
| C. | 两个有理数的差不大于被减数 | |
| D. | 多个有理数相乘,有奇数个负因式时积为负 |
8.下列运算中正确的是( )
| A. | 3a+2a=5a2 | B. | -x2•(-x)3=(-x)5 | C. | 2a2•a3=2a6 | D. | (a-b)(b-a)=-(a-b)2 |
5.下列说法中错误的是( )
| A. | 4的算术平方根是2 | B. | 负数有立方根,并且是负数 | ||
| C. | 8的立方根是±2 | D. | -1的立方根是-1 |
3.下列说法中,正确的是( )
| A. | 64的平方根是8 | B. | 4的平方根是2或-2 | ||
| C. | (-3)2没有平方根 | D. | 16的平方根是4和-4 |
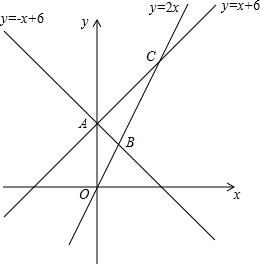 如图,直线y=-x+6交直线y=x+6于点A,直线y=-x+6与直线y=2x相交于点B,直线y=x+6与直线y=2x相交于点C.
如图,直线y=-x+6交直线y=x+6于点A,直线y=-x+6与直线y=2x相交于点B,直线y=x+6与直线y=2x相交于点C.