题目内容
5.已知二次函数y=x2+bx+c的图象过点A(c,0),对称轴是x=2(1)写出二次函数y=x2+bx+c的三条性质;
(2)求一元二次方程x2+bx+c=0的解.
分析 (1)根据待定系数法,可得函数解析式,根据a、b、c的值可得函数的性质;
(2)根据解方程,可得答案.
解答 解:(1)由二次函数y=x2+bx+c的图象过点A(c,0),对称轴是x=2,得
$\left\{\begin{array}{l}{-\frac{b}{2}=2}\\{{c}^{2}+bc+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-4}\\{c=0}\end{array}\right.$或$\left\{\begin{array}{l}{b=-4}\\{c=3}\end{array}\right.$,
①当b=-4,c=0时,y=x2+bx+c函数有最小值y=-4;当x<2时,y随x的增大而减小,当x>2时,y随x的增大而增大;函数图象过原点;
②当b=-4,c=3时,y=x2+bx+c函数有最小值y=-1;当x<2时,y随x的增大而减小,当x>2时,y随x的增大而增大;函数图象开口向上;
(2)当b=-4,c=0时,x2-4x=0,解得x=0,或x=4;
当b=-4,c=3时,x2-4x+3=0,解得x=1或x=3.
点评 本题考查了二次函数的性质,利用待定系数法求函数解析式,分类讨论是解题关键,以防遗漏.

练习册系列答案
相关题目




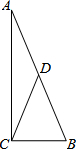 如图,在△ABC中,∠C=90°,点D为AB的中点,BC=3,AB=9,△DBC沿着CD翻折后,点B落到点E,那么AE的长为7.
如图,在△ABC中,∠C=90°,点D为AB的中点,BC=3,AB=9,△DBC沿着CD翻折后,点B落到点E,那么AE的长为7.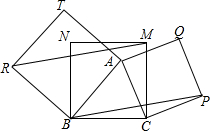 如图,正方形MNBC内有一点A,以AB,AC为边向△ABC外作正方形ABRT和正方形ACPQ,连结RM,BP.求证:BP∥RM.
如图,正方形MNBC内有一点A,以AB,AC为边向△ABC外作正方形ABRT和正方形ACPQ,连结RM,BP.求证:BP∥RM.