题目内容
16.在平面直角坐标系中,A(a,b),B(2,2),且|a-b+8|+$\sqrt{3a+2b-6}$=0.(1)求点A的坐标;
(2)过点A作AC⊥x轴于点C,连接BC,AB,求三角形ABC的面积;
(3)在(2)的条件下,延长AB交x轴于点D,AB交y轴于点E,那么OD与OE是否相等,请说明理由.
分析 (1)利用非负数的性质解得a,b,即可得点A的坐标;
(2)利用梯形和三角形的面积公式,用梯形ACFB的面积-三角形BCF的面积即可得到三角形ABC的面积;
(3)利用(2)的结论可得OD的长,利用三角形EOD的面积=三角形ACD的面积-梯形ACOE的面积可得OE的长.
解答 解:(1)由|a-b+8|+$\sqrt{3a+2b-6}$=0,得
$\left\{\begin{array}{l}{a-b+8=0}\\{3a+2b-6=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-2}\\{b=6}\end{array}\right.$.
∴点A的坐标为(-2,6);
(2)如图1,过B作BF⊥x轴于F,三角形ABC的面积=梯形ACFB的面积-三角形BCF的面积
=$\frac{1}{2}(BF+AC)•CF-\frac{1}{2}•CF•BF$
=$\frac{1}{2}$(2+6)×4$-\frac{1}{2}×4×2$
=12;
(3)如图2,OD与OE相等. 理由如下:
理由如下:
设点D的坐标为(x,0)(x>0),点E的坐标为(0,y)(y>0),
则CD=x+2,OE=y,
因为,三角形ABC的面积=三角形ACD的面积-三角形BCD的面积,
所以,12=$\frac{1}{2}×(x+2)×6-\frac{1}{2}×(x+2)×2$=2(x+2),
解得,x=4,即OD=4.
又因为,三角形EOD的面积=三角形ACD的面积-梯形ACOE的面积,
所以,$\frac{1}{2}×4×y=\frac{1}{2}×6×6-\frac{1}{2}×(y+6)×2$,
解得:y=4,即OE=4,
所以,OD=OE.
点评 本题主要考查了三角形的面积和非负数的性质,根据题意画出图形是解答此题的关键.

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案| A. | 30.07×104 | B. | 3.007×105 | C. | 300.7×103 | D. | 0.3007×106 |
 在一幅长80厘米,宽50厘米的矩形风景画的四周镶一条金色的纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400平方厘米,设金色纸边的宽为x厘米,那么满足的方程是( )
在一幅长80厘米,宽50厘米的矩形风景画的四周镶一条金色的纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400平方厘米,设金色纸边的宽为x厘米,那么满足的方程是( )| A. | x2+130x-1400=0 | B. | x2-130x-1400=0 | C. | x2+65x-350=0 | D. | x2-65x-350=0 |
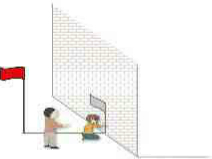 小聪和他的同学利用影长测量旗杆高度(如图),当1m长的直立竹竿的影长为1.5m时,测量旗杆落在地上的影长为21m,落在墙上的影长为2m,求旗杆的高度.
小聪和他的同学利用影长测量旗杆高度(如图),当1m长的直立竹竿的影长为1.5m时,测量旗杆落在地上的影长为21m,落在墙上的影长为2m,求旗杆的高度.