题目内容
14.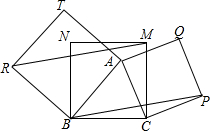 如图,正方形MNBC内有一点A,以AB,AC为边向△ABC外作正方形ABRT和正方形ACPQ,连结RM,BP.求证:BP∥RM.
如图,正方形MNBC内有一点A,以AB,AC为边向△ABC外作正方形ABRT和正方形ACPQ,连结RM,BP.求证:BP∥RM.
分析 连接PM,RN,根据正方形的性质证明△ABC≌△PMC(SAS),得到PM=AB,所以PM=BR,再证明△BCP≌△MNR (SAS),得到BP=MR,所以得到平行四边形BPMR,所以BP∥RM.
解答 证明:如图,连接PM,RN,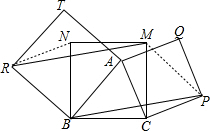
∵正方形MNBC、正方形ABRT、正方形ACPM,
∴MN=MC=BC,AB=BR,AC=PC,∠BCM=∠ABR=∠BNM=∠ACP=90°
∵∠ACB=∠BCM-∠ACM,∠PCM=∠ACP-∠ACM,
∴∠ACB=∠PCM,
在△ABC和△PMC中,
$\left\{\begin{array}{l}{BC=BM}\\{∠ACB=∠PCM}\\{AC=PC}\end{array}\right.$
∴△ABC≌△PMC(SAS),
∴PM=AB,
∴PM=BR,
同理可得:RN=AC,∠BNR=∠ACB,
∴RN=PC,∠BNR=∠PCM,
∵∠BCP=∠BCM+∠PCM,∠MNR=∠BNM+∠BNR
∴∠BCP=∠MNR,
在△BCP和△MNR中,
$\left\{\begin{array}{l}{RN=PC}\\{∠BCP=∠MNR}\\{MN=BC}\end{array}\right.$
∴△BCP≌△MNR (SAS)
∴BP=MR
∴四边形BPMR为平行四边形,
∴BP∥RM
点评 本题考查考查了全等三角形的性质与判定定理,正方形的性质,平行四边形的判定,解决本题的关键是证明四边形BPMR为平行四边形.

练习册系列答案
相关题目
4.2014年我省通过实施土地整治项目,累计新增耕地30.07万亩,30.07万用科学记数法表示正确的是( )
| A. | 30.07×104 | B. | 3.007×105 | C. | 300.7×103 | D. | 0.3007×106 |
6. 在一幅长80厘米,宽50厘米的矩形风景画的四周镶一条金色的纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400平方厘米,设金色纸边的宽为x厘米,那么满足的方程是( )
在一幅长80厘米,宽50厘米的矩形风景画的四周镶一条金色的纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400平方厘米,设金色纸边的宽为x厘米,那么满足的方程是( )
 在一幅长80厘米,宽50厘米的矩形风景画的四周镶一条金色的纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400平方厘米,设金色纸边的宽为x厘米,那么满足的方程是( )
在一幅长80厘米,宽50厘米的矩形风景画的四周镶一条金色的纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400平方厘米,设金色纸边的宽为x厘米,那么满足的方程是( )| A. | x2+130x-1400=0 | B. | x2-130x-1400=0 | C. | x2+65x-350=0 | D. | x2-65x-350=0 |
3.一射击运动员在一次射击练习中打出的成绩是(单位:环):7,8,9,8,6,8,10,7,这组数据的众数和中位数分别是( )
| A. | 8,8 | B. | 7,8 | C. | 8,7 | D. | 7,7.5 |
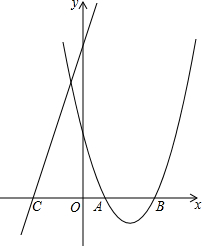 已知抛物线y=x2-(k+2)x+$\frac{5k+2}{4}$和直线y=(k+1)x+(k+1)2
已知抛物线y=x2-(k+2)x+$\frac{5k+2}{4}$和直线y=(k+1)x+(k+1)2 求阴影部分的面积.(单位:厘米)
求阴影部分的面积.(单位:厘米) 已知有理数a,b在数轴上的位置如图所示,请比较 a,b,|a|,|b|的大小(用<连接起来).
已知有理数a,b在数轴上的位置如图所示,请比较 a,b,|a|,|b|的大小(用<连接起来).