Question

10．如图（1），已知Rt△ABC的直角边AC的长为2，以AC为直径的⊙O与斜边AB交于点D，过D作⊙O的切线交BC于点E．
（1）求证：BE=DE；
（2）延长DE与AC的延长线交于点F，若DF=$\sqrt{3}$，求△ABC的面积；
（3）连接OE如图（2），当∠CAB为何值时，四边形AOED为平行四边形，并说明理由．

Answer 1

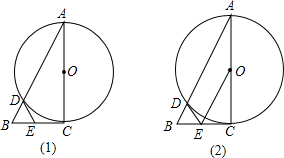
分析 （1）如图（1）a，连接OD．根据切线的性质可得OD⊥DE，从而可得∠AD0+∠BDE=90°．由∠ACB=90°可得∠BAC+∠B=90°．由OA=OD可得∠BAC=∠ADO，根据等角的余角相等可得∠BDE=∠B，从而可得BE=DE；
（2）如图（1）b，在Rt△ODF中运用三角函数可得∠DOF=60°，根据圆周角定理可得∠DAC=30°．在Rt△ACB中运用三角函数可求出BC，即可求出△ACB的面积；
（3）当∠CAB=45°时，根据圆周角定理可得$∠\\;DOC=90°$DOC=90°，从而可证到四边形DOCE是正方形，则有DE∥OC，∠EOC=45°，即可得到∠EOC=∠BAC=45°，则有AB∥OE，即可得到四边形AOED为平行四边形．

解答 解：（1）如图（1）a，连接OD．

∵DE与⊙O相切于点D，
∴OD⊥DE，
∴∠AD0+∠BDE=90°．
∵∠ACB=90°，
∴∠BAC+∠B=90°．
∵OA=OD，
∴∠BAC=∠ADO，
∴∠BDE=∠B，
∴BE=DE；

（2）如图（1）b，

在Rt△ODF中，
∵DF=$\sqrt{3}$，DO=$\frac{1}{2}$AC=1，
∴tan∠DOF=$\frac{DF}{DO}$=$\sqrt{3}$，
∴∠DOF=60°，
∴∠DAC=30°．
在Rt△ACB中，
由tan∠BAC=$\frac{BC}{AC}$得，
BC=AC•tan∠BAC=2×$\frac{\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$，
∴S_△ACB=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×2×$\frac{2\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$；

（3）如图（2），

当∠CAB=45°时，四边形AOED为平行四边形，
理由如下：
∵∠CAB=45°，
∴$∠\\;DOC=90°$DOC=90°，
∴∠ODE=∠OCE=∠DOC=90°，
∴四边形DOCE是矩形．
∵OD=OC，∴矩形DOCE是正方形，
∴DE∥OC，∠EOC=45°，
∴∠EOC=∠BAC=45°，
∴AB∥OE，
∴四边形AOED为平行四边形．

点评 本题主要考查了切线的性质、圆周角定理、三角函数的定义、特殊角的三角函数值、等角的余角相等、平行四边形的判定、矩形的判定、正方形的判定等知识，运用三角函数是解决第（2）小题的关键，证到四边形DOCE是正方形是解决第（3）小题的关键．