题目内容
14．利用乘法公式计算：（1）（2x-y）2-4（x-y）（x+2y）
（2）（a-2b-3c）（a-2b+3c）
分析 （1）根据平方差公式，即可解答；
（2）根据平方差公式，即可解答．
解答 解：（1）原式=4x2-4xy+y2-4（x2-2xy-xy-2y2）
=4x2-4xy+y2-4x2-8xy+4xy+8y2
=-8xy+9y2．
（2）原式=[（a-2b）-3c][（a-2b+3c]
=a2+4b2-4ab-9c2．
点评 本题考查了平方差公式，解决本题的关键是熟记平方差公式．
练习册系列答案
相关题目
5．若$\sqrt{{-（1-a）}^{2}}$有意义，则满足条件的a的个数为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
2．若$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}{2x+y=m}\\{x-ny=3}\end{array}\right.$的解，则m，n的值为（ ）
| A． | 3，1 | B． | 3，-1 | C． | -3，1 | D． | -3，-1 |
二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论；①2a+b＞0；②abc＜0；③b2-4ac＞0；④a+b+c＜0；⑤4a-2b+c＜0；⑥若（x1，y1）、（x2，y2）在函数图象上，当x1＜x2＜1时，y1＜y2，其中正确的个数是（ ）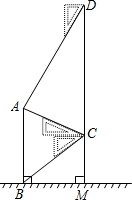
如图，某中学在教学楼前新建了一座雕塑AB．为了测量雕塑的高度，小明在二楼找到一点C，利用三角尺测得雕塑顶端点A的仰角为30°，底部点B的俯角为45°，小华在五楼找到一点D，利用三角尺测得点A的俯角为60°．若CD为9.6m，则雕塑AB的高度为多少？（结果精确到0.1m，参考数据：$\sqrt{3}$≈1.73）．
3．事件“反比例函数y=$\frac{k}{x}$（k＞0）经过点（0，3）”的概率是（ ）
| A． | 0 | B． | $\frac{1}{3}$ | C． | $\frac{1}{k}$ | D． | 1 |