题目内容
18.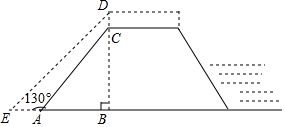 为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即CD=2米),背水坡DE的坡度i=1:1(即DB:EB=1:1),如图所示,已知AE=4米,∠EAC=130°,求水坝原来的高度BC.
为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即CD=2米),背水坡DE的坡度i=1:1(即DB:EB=1:1),如图所示,已知AE=4米,∠EAC=130°,求水坝原来的高度BC.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)
分析 设BC=x米,用x表示出AB的长,利用坡度的定义得到BD=BE,进而列出x的方程,求出x的值即可.
解答 解:设BC=x米,
在Rt△ABC中,
∠CAB=180°-∠EAC=50°,
AB=$\frac{BC}{tan50°}$≈$\frac{BC}{1.2}$=$\frac{5BC}{6}$=$\frac{5}{6}$x,
在Rt△EBD中,
∵i=DB:EB=1:1,
∴BD=BE,
∴CD+BC=AE+AB,
即2+x=4+$\frac{5}{6}$x,
解得x=12,
即BC=12,
答:水坝原来的高度为12米.
点评 本题考查了解直角三角形的应用,解答本题的关键是理解坡度、坡比的含义,构造直角三角形,利用三角函数表示相关线段的长度,难度一般.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
8. 如图,⊙O中,弦AB、CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是( )
如图,⊙O中,弦AB、CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是( )
 如图,⊙O中,弦AB、CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是( )
如图,⊙O中,弦AB、CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是( )| A. | 43° | B. | 35° | C. | 34° | D. | 44° |
9.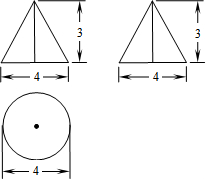 如图是一个几何体的三视图,则该几何体的侧面积是( )
如图是一个几何体的三视图,则该几何体的侧面积是( )
 如图是一个几何体的三视图,则该几何体的侧面积是( )
如图是一个几何体的三视图,则该几何体的侧面积是( )| A. | $2\sqrt{13}π$ | B. | 10π | C. | 20π | D. | $4\sqrt{13}π$ |
6. 如图,直线a∥b,c⊥a,则c与b相交所形成的∠1的度数为( )
如图,直线a∥b,c⊥a,则c与b相交所形成的∠1的度数为( )
 如图,直线a∥b,c⊥a,则c与b相交所形成的∠1的度数为( )
如图,直线a∥b,c⊥a,则c与b相交所形成的∠1的度数为( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
3.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (-a2)3=-a5 | C. | a10÷a9=a(a≠0) | D. | (-bc)4÷(-bc)2=-b2c2 |