题目内容
15.已知一次函数y=kx-4,当x=2时,y=-3.(!)求一次函数的解析式;
(2)将该函数的图象向上平移6个单位,平移后的图象与两坐标轴交点分别为A和B,则AB的距离为多少?
分析 (1)根据待定系数法解出解析式即可;
(2)根据一次函数的几何变换得出解析式,再求出交点坐标,由两点间的距离公式求得AB的长度即可.
解答 解:(1)把x=2,y=-3代入y=kx-4中,
可得:-3=2k-4,
解得:k=$\frac{1}{2}$,
所以一次函数的解析式为:y=$\frac{1}{2}$x-4;
(2)一次函数y=$\frac{1}{2}$x-4的图象向上平移6个单位后的解析式为:y=$\frac{1}{2}$x-4+6=$\frac{1}{2}$x+2,
把x=0,y=0分别代入y=$\frac{1}{2}$x+2中,
可得图象与坐标轴的交点坐标为A(0,2),(-4,0),
所以AB=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$.
点评 本题考查了待定系数法求一次函数的解析式、一次函数图象与几何变换.解题的关键是待定系数法求函数解析式.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
3.若物体运动的路程s(米)与时间t(秒)的关系式为s=3t2+2t+1,则当t=4秒时,该物体所经过的路程为( )
| A. | 28米 | B. | 48米 | C. | 57米 | D. | 88米 |
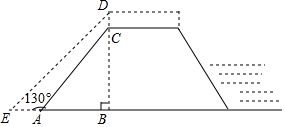 为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即CD=2米),背水坡DE的坡度i=1:1(即DB:EB=1:1),如图所示,已知AE=4米,∠EAC=130°,求水坝原来的高度BC.
为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即CD=2米),背水坡DE的坡度i=1:1(即DB:EB=1:1),如图所示,已知AE=4米,∠EAC=130°,求水坝原来的高度BC.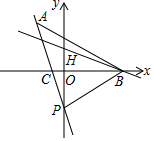 如图,已知一次函数y=kx+b的图象经过点A(-2,5),并且与x轴交于点C,与y轴交于点P;直线y=-$\frac{1}{2}$x+3与x轴交于点B,与y轴交于点H,点H恰好与点P关于x轴对称.
如图,已知一次函数y=kx+b的图象经过点A(-2,5),并且与x轴交于点C,与y轴交于点P;直线y=-$\frac{1}{2}$x+3与x轴交于点B,与y轴交于点H,点H恰好与点P关于x轴对称.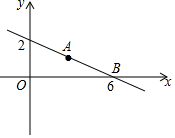 如图,直线y=kx+b经过点A(3,1)和点B(6,0)两点,则不等式0≤kx+b<$\frac{1}{3}$x的解集为1<x≤6.
如图,直线y=kx+b经过点A(3,1)和点B(6,0)两点,则不等式0≤kx+b<$\frac{1}{3}$x的解集为1<x≤6. 已知二次函数y=ax2+2ax+a-1(a>0).
已知二次函数y=ax2+2ax+a-1(a>0).