题目内容
19.解方程:$\sqrt{2}$x2-4x=4$\sqrt{2}$(配方法).分析 先把二次项系数化为1,再利用配方法得到(x-$\sqrt{2}$)2=6,然后利用直接开平方法解方程.
解答 解:x2-2$\sqrt{2}$x=4,
x2-2$\sqrt{2}$x+($\sqrt{2}$)2=4+($\sqrt{2}$)2,
(x-$\sqrt{2}$)2=6,
x-$\sqrt{2}$=±$\sqrt{6}$,
所以x1=$\sqrt{2}$+$\sqrt{6}$,x2=$\sqrt{2}$-$\sqrt{6}$.
点评 本题考查了解一元二次方程-配方法:将一元二次方程配成(x+m)2=n的形式,再利用直接开平方法求解,这种解一元二次方程的方法叫配方法.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
相关题目
13.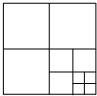 如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪成四个小正方形,如此继续下去,…,请你根据以上操作方法得到的正方形的个数的规律完成各题.
如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪成四个小正方形,如此继续下去,…,请你根据以上操作方法得到的正方形的个数的规律完成各题.
(1)将下表填写完整;
(2)an=3n+1(用含n的代数式表示);
(3)按照上述方法,能否得到2015个正方形?如果能,请求出n;如果不能,请简述理由.
 如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪成四个小正方形,如此继续下去,…,请你根据以上操作方法得到的正方形的个数的规律完成各题.
如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪成四个小正方形,如此继续下去,…,请你根据以上操作方法得到的正方形的个数的规律完成各题.(1)将下表填写完整;
| 操作次数N | 1 | 2 | 3 | 4 | 5 | … | n |
| 正方形个数 | 4 | 7 | 10 | an |
(3)按照上述方法,能否得到2015个正方形?如果能,请求出n;如果不能,请简述理由.