题目内容
1．一个等腰三角形的两条边长为3，8，那么这个等腰三角形的周长是（ ）| A． | 19 | B． | 14 | C． | 19或14 | D． | 以上均有可能 |
分析 题目给出等腰三角形有两条边长为8和3，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．
解答 解：当腰为8时，周长=8+8+3=19；
当腰长为3时，根据三角形三边关系可知此情况不成立；
根据三角形三边关系可知：等腰三角形的腰长只能为8，这个三角形的周长是19．
故选：A．
点评 本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．
练习册系列答案
相关题目
11．下列说法正确的是（ ）
| A． | 23表示2×3的积 | |
| B． | 任何一个有理数的偶次方是正数 | |
| C． | 一个数的平方是$\frac{4}{9}$，这个数一定是$\frac{2}{3}$ | |
| D． | -32与（-3）2互为相反数 |
9．下面是一组按规律排列的数：1，2，4，8，16，…，则第2013个数是（ ）
| A． | 22009 | B． | 22010 | C． | 22011 | D． | 22012 |
16．若二次根式$\sqrt{3x+1}$在实数范围内有意义，则x的取值范围是（ ）
| A． | x≤-$\frac{1}{3}$ | B． | x≥-$\frac{1}{3}$ | C． | x≠-$\frac{1}{3}$ | D． | x≥0 |
6．
如图，在4×4的网格中，将△ABC绕B顺时针旋转90°得到△BDE，则A走过的路径的长是（ ）
如图，在4×4的网格中，将△ABC绕B顺时针旋转90°得到△BDE，则A走过的路径的长是（ ）| A． | π | B． | 2π | C． | 3π | D． | 1.5π |
13．若关于x的方程（2x-t）2-47=0的两个根均为正数，则t的最小整数值是（ ）
| A． | 1 | B． | 6 | C． | 7 | D． | 8 |
10．
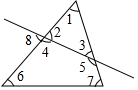如图，按各角的位置，下列判断错误的是（ ）
如图，按各角的位置，下列判断错误的是（ ）| A． | ∠5与∠8是同位角 | B． | ∠5与∠6是同旁内角 | ||
| C． | ∠3与∠4是内错角 | D． | ∠1与∠2是同旁内角 |