题目内容
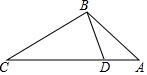
6．
如图，在4×4的网格中，将△ABC绕B顺时针旋转90°得到△BDE，则A走过的路径的长是（ ）| A． | π | B． | 2π | C． | 3π | D． | 1.5π |
分析 由每个小正方形的边长都为1，可求得AB长，然后由弧长公式，求得答案．
解答 解：∵每个小正方形的边长都为1，
∴AB=4，
∵将△ABC绕点B顺时针旋转90°得到△BDE，
∴∠ABE=90°，
∴A点运动的路径$\widehat{AE}$的长为：$\frac{90•π×4}{180}$=2π．
故选B．
点评 此题考查了旋转的性质以及弧长公式的应用．注意确定半径与圆心角是解此题的关键．
练习册系列答案
相关题目
16．在Rt△ABC中，∠C=90°，AB=15，sinA=$\frac{1}{3}$，则BC=（ ）
| A． | 5 | B． | 10$\sqrt{2}$ | C． | 45 | D． | $\frac{1}{5}$ |
17．在某次聚会上，每两人都握了一次手，所有人共握了10次，设有x人参加这次聚会，则列出方程正确的是（ ）
| A． | x（x+1）=10 | B． | $\frac{x（x+1）}{2}$=10 | C． | x（x-1）=10 | D． | $\frac{x（x-1）}{2}$=10 |
14．
如图，点D在△ABC的边AC上，要判定△ADB与△ABC相似，添加一个条件，不正确的是（ ）
如图，点D在△ABC的边AC上，要判定△ADB与△ABC相似，添加一个条件，不正确的是（ ）| A． | ∠ABD=∠C | B． | ∠ADB=∠ABC | C． | $\frac{AB}{BD}=\frac{CB}{CA}$ | D． | $\frac{AB}{AD}=\frac{AC}{AB}$ |
1．一个等腰三角形的两条边长为3，8，那么这个等腰三角形的周长是（ ）
| A． | 19 | B． | 14 | C． | 19或14 | D． | 以上均有可能 |
如图，直线AB，CD相交于O，OE平分∠AOD，∠FOC=100°，∠1=40°，求∠2和∠3的度数．
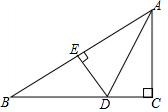如图，在Rt△ABC中，∠C=90°，AD平分∠CAB，DE⊥AB于E，AC=3，BC=4．
16．
如图，已知AB∥DE，∠ABC=65°，∠CDE=138°，则∠C的值为（ ）
如图，已知AB∥DE，∠ABC=65°，∠CDE=138°，则∠C的值为（ ）| A． | 21° | B． | 23° | C． | 25° | D． | 30° |