题目内容
13.若关于x的方程(2x-t)2-47=0的两个根均为正数,则t的最小整数值是( )| A. | 1 | B. | 6 | C. | 7 | D. | 8 |
分析 先利用直接开平方法得到x1=$\frac{t+\sqrt{47}}{2}$,x2=$\frac{t-\sqrt{47}}{2}$,则根据题意得到t>$\sqrt{47}$,然后利用无理数估算确定t的最小整数值.
解答 解:(2x-t)2=47,
2x-t=±$\sqrt{47}$,
所以x1=$\frac{t+\sqrt{47}}{2}$,x2=$\frac{t-\sqrt{47}}{2}$,
因为方程的两个根均为正数,
所以t>$\sqrt{47}$,
所以t的最小整数值是7.
故选C.
点评 本题考查了直接开平方法解方程.也考查了无理数的估算.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
1.一个等腰三角形的两条边长为3,8,那么这个等腰三角形的周长是( )
| A. | 19 | B. | 14 | C. | 19或14 | D. | 以上均有可能 |
8.下列二次根式中可以和$\sqrt{2}$相加合并的是( )
| A. | $\sqrt{14}$ | B. | $\sqrt{18}$ | C. | $\sqrt{\frac{1}{3}}$ | D. | $\sqrt{12}$ |
5.-9的倒数是( )
| A. | 9 | B. | -9 | C. | $\frac{1}{9}$ | D. | $-\frac{1}{9}$ |
2.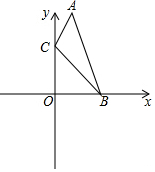 如图,在直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,当△ABC的周长最小时点C的坐标是( )
如图,在直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,当△ABC的周长最小时点C的坐标是( )
 如图,在直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,当△ABC的周长最小时点C的坐标是( )
如图,在直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,当△ABC的周长最小时点C的坐标是( )| A. | (0,3) | B. | (0,2) | C. | (0,1) | D. | (0,0) |
3.|3.14-π|的计算结果是( )
| A. | 0 | B. | π-3.14 | C. | 3.14-π | D. | -3.14-π |
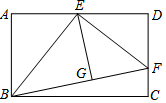 如图,已知矩形ABCD中,点E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,连接EF,若AB=6,BC=4$\sqrt{6}$,则下列说法中正确的个数有( )
如图,已知矩形ABCD中,点E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,连接EF,若AB=6,BC=4$\sqrt{6}$,则下列说法中正确的个数有( )