题目内容
5. 如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )
如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )| A. | $\sqrt{6}$ | B. | 2$\sqrt{6}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 连接BP.由正方形的对称性可知PD=PB,则PD+PE=PB+PE,依据两点之间线段最短可知当点B、P、E在一条直线上时,PD+PE有最小值,最小值=BE,然后依据正方形和等边三角形的性质求解即可
解答 解:连接BP.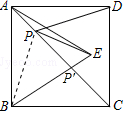
∵点B与D关于AC对称,
∴PD=PB,
∴PD+PE=PB+PE.
∴由两点之间线段最短可知当点P为点P′处时,PD+PE有最小值,最小值=BE.
∵正方形ABCD的面积为12,
∴AB=2$\sqrt{3}$.
又∵△ABE是等边三角形,
∴BE=AB=2$\sqrt{3}$.
∴PD+PE的最小值为2$\sqrt{3}$.
故选:D.
点评 本题主要考查的是正方形的性质、轴对称-最短路径问题,等边三角形的性质,等腰三角形的性质,明确当点P、E、B在一条直线上是,PE+PD有最小值是解题的关键.

练习册系列答案
相关题目
16.下列式子中正确的是( )
| A. | -3-2=-1 | B. | 3a+2b=5ab | C. | -(-7)=7 | D. | 5xy-xy=5 |
13.把方程x2-6x+4=0的左边配成完全平方,正确的变形是( )
| A. | (x-3)2=9 | B. | (x-3)2=13 | C. | (x+3)2=5 | D. | (x-3)2=5 |
20.篮球比赛中,要求每两队之间都进行一场比赛,总共比赛21场,问有多少个队参加比赛?设有x个队参加比赛,则可列方程为( )
| A. | 1+x+x2=21 | B. | x2+2x=21 | C. | x(x-1)=21 | D. | $\frac{1}{2}$x(x-1)=21 |
15.在平面直角坐标系中,点P(3,-1)关于x轴对称的点的坐标是( )
| A. | (-3,-1) | B. | (-3,1) | C. | (-1,3) | D. | (3,1) |
 如图,点C在线段AB上,点M、N分别是AC、BC的中点.
如图,点C在线段AB上,点M、N分别是AC、BC的中点. 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(2,3),B(3,1),C(-2,-2).
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(2,3),B(3,1),C(-2,-2). 在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,9).
在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,9). 一个能储水30升的电热水器,安装有一个进水管和一个出水管,进出水管每单位时间内进出的水量各自是一个定值.设从某时刻开始的4分钟内只补充进水而不出水,在随后的8分钟内出水的同时补充进水,得到容器中剩余水量y(升)与时间x(分)之间的函数关系如图所示.根据图象信息回答下列问题:
一个能储水30升的电热水器,安装有一个进水管和一个出水管,进出水管每单位时间内进出的水量各自是一个定值.设从某时刻开始的4分钟内只补充进水而不出水,在随后的8分钟内出水的同时补充进水,得到容器中剩余水量y(升)与时间x(分)之间的函数关系如图所示.根据图象信息回答下列问题: