题目内容
13.抛物线y=ax2+bx+c与x轴的公共点是(-2,0),(6,0),则此抛物线的对称轴是x=2.分析 因为点(-2,0),(6,0)的纵坐标都为0,所以可判定是一对对称点,把两点的横坐标代入公式x=$\frac{{x}_{1}+{x}_{2}}{2}$求解即可.
解答 解:
∵抛物线与x轴的交点为(-2,0),(6,0),
∴两交点关于抛物线的对称轴对称,
则此抛物线的对称轴是直线x=$\frac{-2+6}{2}$=2,即x=2.
故答案是:x=2.
点评 本题考查了抛物线与x轴的交点,以及如何求二次函数的对称轴,对于此类题目可以用公式法也可以将函数化为顶点式来求解,也可以用公式x=$\frac{{x}_{1}+{x}_{2}}{2}$求解,即抛物线y=ax2+bx+c与x轴的交点是(x1,0),(x2,0),则抛物线的对称轴为直线x=$\frac{{x}_{1}+{x}_{2}}{2}$.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
3.若关于x的一元二次方程(m-2)x2+5x+m2-3m+2=0有一根为0,则m值为( )
| A. | 1 | B. | 0 | C. | 1或2 | D. | 2 |
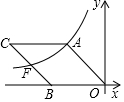 如图,O为坐标原点,四边形OACB是菱形,点B在x轴的负半轴上,sin∠AOB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$在第二象限内的图象经过点A,与BC交于点F,若△AOF的面积为20,则该反比例函数的表达式为y=$\frac{24}{x}$.
如图,O为坐标原点,四边形OACB是菱形,点B在x轴的负半轴上,sin∠AOB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$在第二象限内的图象经过点A,与BC交于点F,若△AOF的面积为20,则该反比例函数的表达式为y=$\frac{24}{x}$. 如图,长方体的长为4厘米,宽为3厘米,高为5厘米.
如图,长方体的长为4厘米,宽为3厘米,高为5厘米.