题目内容
5.(1)化简$\frac{{x}^{2}}{x-1}$+$\frac{1}{1-x}$;(2)先化简,再求值:(x-2-$\frac{12}{x+2}$)÷$\frac{4-x}{x+2}$,其中x2=4.
分析 (1)通分后因式分解,然后约分;
(2)先将括号内的部分通分,然后将除法转化为乘法,约分后代入求值.
解答 解:(1)原式=$\frac{{x}^{2}}{x-1}$-$\frac{1}{x-1}$
=$\frac{{x}^{2}-1}{x-1}$
=$\frac{(x-1)(x+1)}{x-1}$
=x+1;
(2)原式=($\frac{{x}^{2}-4}{x+2}$-$\frac{12}{x+2}$)•$\frac{x+2}{4-x}$
=$\frac{(x-4)(x+4)}{x+2}$•$\frac{x+2}{4-x}$
=-x-4.
∵x2=4,
∴x=±2,
当x=-2时,分式无意义,则x=2;
当x=-2时,原式=2-4=-2.
点评 本题主要考查了分式的化简求值,熟悉通分、约分、因式分解是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列计算正确的是( )
| A. | x2+x4=x6 | B. | x•x2=x3 | C. | x6÷x3=x2 | D. | (-x2y)2=x6y3 |

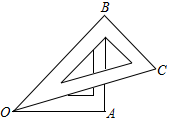 如图,将一副三角板摆放在一起
如图,将一副三角板摆放在一起