题目内容
11.不改变分式的值,使下列分式的分子和分母都不含“-”号.(1)-$\frac{-{x}^{3}y}{3a{b}^{2}}$=$\frac{{x}^{3}y}{3a{b}^{2}}$;
(2)-$\frac{-{a}^{3}}{-17{b}^{2}}$=-$\frac{{a}^{3}}{17{b}^{2}}$;
(3)$\frac{-5a}{-13{x}^{2}}$=$\frac{5a}{13{x}^{2}}$.
分析 (1)根据分式的分子、分母及分式的符号,同时改变两个其值不变,可得答案;
(2)根据分式的分子、分母及分式的符号,同时改变两个其值不变,可得答案;
(3)根据分式的分子、分母及分式的符号,同时改变两个其值不变,可得答案.
解答 解:(1)改变分子、分式的符号,得
原式=$\frac{{x}^{3}y}{3a{b}^{2}}$;
(2)改变分子、分母的符号,得
原式=-$\frac{{a}^{3}}{17{b}^{2}}$;
(3)改变分子、分母的符号,得
原式=$\frac{5a}{13{x}^{2}}$.
故答案为:$\frac{{x}^{3}y}{3a{b}^{2}}$;-$\frac{{a}^{3}}{17{b}^{2}}$;$\frac{5a}{13{x}^{2}}$.
点评 本题考查了分式的基本性质,分式的分子、分母及分式的符号,同时改变两个其值不变.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
19.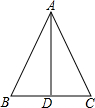 下列条件中能使△ABD≌△ACD的是( )
下列条件中能使△ABD≌△ACD的是( )
 下列条件中能使△ABD≌△ACD的是( )
下列条件中能使△ABD≌△ACD的是( )| A. | AB=AC,∠B=∠C | B. | AB=AC,∠ADB=∠ADC | C. | AB=AC,∠BAD=∠CAD | D. | BD=CD,∠BAD=∠CAD |
3.-3减去-$\frac{7}{5}$与-$\frac{3}{5}$的和的结果是( )
| A. | -$\frac{19}{5}$ | B. | -$\frac{11}{5}$ | C. | -5 | D. | -1 |
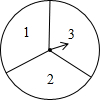 2015年1月9日,2014年度国家科学技术奖励大会在北京人民大会堂举行.为了加强青少年科技创新的意识,某市举办了科学表演大赛.小丽和小红想利用转转盘的游戏决定谁去参加该大赛,游戏规则如下:如图是一个可以自由转动的转盘,被平均分成3个扇形,扇形上分别标有数字1,2,3,转动一次转盘,任其自由停止,指针会指向某个扇形(若指针指在分界线上,则重转),相应地得到一个数字,两人各转动一次,若得到的两个数字之和为偶数,则小丽去参赛,否则小红去参赛.
2015年1月9日,2014年度国家科学技术奖励大会在北京人民大会堂举行.为了加强青少年科技创新的意识,某市举办了科学表演大赛.小丽和小红想利用转转盘的游戏决定谁去参加该大赛,游戏规则如下:如图是一个可以自由转动的转盘,被平均分成3个扇形,扇形上分别标有数字1,2,3,转动一次转盘,任其自由停止,指针会指向某个扇形(若指针指在分界线上,则重转),相应地得到一个数字,两人各转动一次,若得到的两个数字之和为偶数,则小丽去参赛,否则小红去参赛.