题目内容
6.在△ABC中,∠A-∠B=∠C,3∠B=2∠A.(1)求∠A,∠B,∠C的度数;
(2)△ABC按角分类,属于什么三角形?
分析 (1)由题意可知∠A=∠B+∠C,从而可求得∠A=90°,然后可求得∠B、∠C的度数;
(2)∠A,∠B,∠C的度数可判断出三角形的形状.
解答 解:(1)∵∠A-∠B=∠C,
∴∠A=∠B+∠C.
∴∠A=180°×$\frac{1}{2}$=90°.
∵3∠B=2∠A=180°,
∴∠B=60°.
∴∠C=90°-60°=30°.
(2)∵∠A=90°、∠B=60°、∠C=30°,
∴△ABC为直角三角形.
点评 本题主要考查的是三角形内角和定理的应用,掌握三角形的内角和定理是解题的关键.

练习册系列答案
相关题目
17.若x=(-2)×3,则x的倒数是( )
| A. | -$\frac{1}{6}$ | B. | $\frac{1}{6}$ | C. | -$\frac{3}{2}$ | D. | $\frac{2}{3}$ |
15.股民李叔叔上星期五买进某公司1000股票,每股67元,下表为本周内每曰该股票收盘价的涨跌情况(单位:元),其中涨记正,跌记负.
(1)星期三收盘时,每股是多少元?
(2)本周内最高收盘价是每股多少元?最低收盘价为每股多少元?
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +4 | +4.5 | -1 | -2.5 | -6 |
(2)本周内最高收盘价是每股多少元?最低收盘价为每股多少元?
 如图,小明将一张正方形的纸片减去一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,且两次剪下的两个长条的面积正好相等.求最后剩下的图形的面积.
如图,小明将一张正方形的纸片减去一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,且两次剪下的两个长条的面积正好相等.求最后剩下的图形的面积.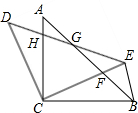 如图,在△ABC中,∠ACB=90°,AC=BC=1,将△ABC绕点C按逆时针方向旋转一定角度,得到△DEC,连接BE.CE交于点F,DE分别交AB,AC于点G,H.
如图,在△ABC中,∠ACB=90°,AC=BC=1,将△ABC绕点C按逆时针方向旋转一定角度,得到△DEC,连接BE.CE交于点F,DE分别交AB,AC于点G,H.