题目内容
9．
已知，如图，?ABCD中，E，F分别是DC，AB边中点，AE，DF交于M点，BE，CF交于N点，连接MN，求证：DC=2MN．
分析 根据平行四边形的性质得到AB=CD，AB∥CD，推出四边形AFED与四边形BFEC是平行四边形，由平行四边形的性质得到FM=DM，FN=CN，根据三角形的中位线的性质即可得到结论．
解答 证明：在?ABCD中，
∵AB=CD，AB∥CD，
∵E，F分别是DC，AB边中点，
∴CE=DE=AF=BF，
∴四边形AFED与四边形BFEC是平行四边形，
∴FM=DM，FN=CN，
∴DC=2MN．
点评 本题考查了平行四边形的判定和性质，三角形的中位线的性质，熟练掌握平行四边形的判定定理是解题的关键．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
19．下列方程组的解中是二元一次方程组$\left\{\begin{array}{l}{2x+y=2}\\{-x+y=5}\end{array}\right.$的解是（ ）
| A． | $\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=-3}\\{y=2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$ |
20．下列窗花图案中是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
17．下列各数，不是无理数的是（ ）
| A． | 0.5 | |
| B． | $\sqrt{8}$ | |
| C． | 3π | |
| D． | 0.282282228…（两个8之间依次多1个2） |
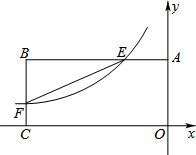如图，反比例函数$y=\frac{k}{x}$（k＜0）的图象与矩形OABC的边相交于E、F两点，连接EF，且BE=2AE，点E坐标为（-2，3）．
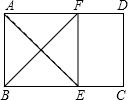如图，在矩形ABCD中，∠A的平分线交BC于E，∠B的平分线交AD于F，求证：四边形ABEF是正方形．
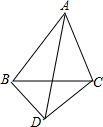在△ABC中，AB=3，∠BAC=60°，把线段BC绕C点逆时针旋转得到线段CD，∠ACB+∠ACD=180°，AD=$\sqrt{19}$，则线段BC的长度为$\frac{\sqrt{31}}{2}$．