题目内容
6.若关于x的方程$\frac{1}{x-1}$-$\frac{a}{2-x}$=$\frac{2(a+1)}{(x-1)(x-2)}$无解,则a的值为多少?分析 去分母化分式方程为整式方程可得(1+a)x=3a+4,分a+1=0、a+1≠0分别讨论求解可得.
解答 解:方程两边都乘以最简公分母(x-1)(x-2)得:x-2+a(x-1)=2(a+1),
整理,得:(1+a)x=3a+4,
①当a+1=0,即a=-1时,方程无解;
②当a+1≠0时,x=$\frac{3a+4}{a+1}$,
∵方程无解,
∴$\frac{3a+4}{a+1}$=1或$\frac{3a+4}{a+1}$=2,
解得:a=-$\frac{3}{2}$或a=-2,
综上,a=-1或a=-$\frac{3}{2}$或a=-2.
点评 本题主要考查分式方程的解,熟知当x的值使分母为0时分式无解是解题的关键.

练习册系列答案
相关题目
19.小红用次数最少的对折方法验证了一条四边形丝巾的形状是正方形,她对折了( )
| A. | 1次 | B. | 2次 | C. | 3次 | D. | 4次 |
15.若一个正多边形的一个外角是40°,则这个正多边形的边数是( )
| A. | 6 | B. | 8 | C. | 9 | D. | 10 |

 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=5,点E在CB边上,以每秒1个单位的速度从点C向点B运动,运动时间为t(s),过点E作AB的平行线,交AC边于点D,以DE为边向上作等边△DEF,设△ABC与△DEF重叠部分的面积为S.
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=5,点E在CB边上,以每秒1个单位的速度从点C向点B运动,运动时间为t(s),过点E作AB的平行线,交AC边于点D,以DE为边向上作等边△DEF,设△ABC与△DEF重叠部分的面积为S.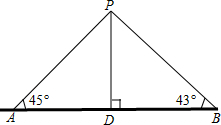 如图,某湖中有一个小岛,湖边有一条笔直的观光小道AB,现决定从小岛建一座与观光小道垂直的小桥PD,测得如下数据:AB=80.0m,∠PAB=45°,∠PBA=43°.求小桥PD的长.(结果精确到0.1m)
如图,某湖中有一个小岛,湖边有一条笔直的观光小道AB,现决定从小岛建一座与观光小道垂直的小桥PD,测得如下数据:AB=80.0m,∠PAB=45°,∠PBA=43°.求小桥PD的长.(结果精确到0.1m)