题目内容
1. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=5,点E在CB边上,以每秒1个单位的速度从点C向点B运动,运动时间为t(s),过点E作AB的平行线,交AC边于点D,以DE为边向上作等边△DEF,设△ABC与△DEF重叠部分的面积为S.
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=5,点E在CB边上,以每秒1个单位的速度从点C向点B运动,运动时间为t(s),过点E作AB的平行线,交AC边于点D,以DE为边向上作等边△DEF,设△ABC与△DEF重叠部分的面积为S.(1)当点F恰好落在AB边上时,求t的值;
(2)当t为何值时,S有最大值?最大值是多少?
分析 (1)由于ED∥AB,得出∠EDC=30°,解直角三角形得出ED=FD=2t,CD=$\sqrt{3}$t,进而求得AD=AC-CD=5$\sqrt{3}$-$\sqrt{3}$t,由等边三角形的性质求得∠ADF=90°,解直角三角形求得AD=$\sqrt{3}$DF=2$\sqrt{3}$t,从而得出5$\sqrt{3}$-$\sqrt{3}$t=2$\sqrt{3}$t,解方程即可求得;
(2)分两种情况,当0<t≤$\frac{5}{3}$时,S就是等边三角形DEF的面积;当$\frac{5}{3}$<t<5时,S就是等边三角形DEF的面积减去等边三角形GHF的面积,再利用配方法写成顶点式,根据二次函数的性质即可求出S的最大值;
解答  解:(1)如图1,∵在Rt△ABC中,∠ACB=90°,∠A=30°,BC=5,DE∥AB,
解:(1)如图1,∵在Rt△ABC中,∠ACB=90°,∠A=30°,BC=5,DE∥AB,
∴∠CDE=∠A=30°,
∴AC=$\sqrt{3}$BC=5$\sqrt{3}$,
∵EC=t,
∴ED=FD=2t,CD=$\sqrt{3}$t,
∴AD=AC-CD=5$\sqrt{3}$-$\sqrt{3}$t,
∵△DEF是等边三角形,
∴∠EDF=60°,
∴∠ADF=90°,
∴AD=$\sqrt{3}$FD=2$\sqrt{3}$t,
∴5$\sqrt{3}$-$\sqrt{3}$t=2$\sqrt{3}$t,
解得t=$\frac{5}{3}$;
(2) 当0<t≤$\frac{5}{3}$时,S=$\frac{1}{2}$•2t•$\frac{\sqrt{3}}{2}$•2t=$\sqrt{3}$t2,
当0<t≤$\frac{5}{3}$时,S=$\frac{1}{2}$•2t•$\frac{\sqrt{3}}{2}$•2t=$\sqrt{3}$t2,
当$\frac{5}{3}$<t<5时,∵AD=AC-CD=5$\sqrt{3}$-$\sqrt{3}$t,
∴DG=$\frac{\sqrt{3}}{3}$AD=5-t,
∵ED=DF=2t,
∴FG=2t-(5-t)=3t-5,
∵ED∥AB,
∴∠FHG=∠FGH=∠EDF=60°,
∴△GFH是等边三角形,
∴S═$\frac{1}{2}$•2t•$\frac{\sqrt{3}}{2}$•2t-$\frac{1}{2}$(3t-5)•$\frac{\sqrt{3}}{2}$•(3t-5)=$\frac{\sqrt{3}}{4}$(2t)2-$\frac{\sqrt{3}}{4}$(3t-5)2=$\frac{5\sqrt{3}}{4}$(t-3)2+5$\sqrt{3}$,
∴t=3时,S有最大值5$\sqrt{3}$.
点评 本题考查了等边三角形的性质,解直角三角形,三角形的面积,二次函数的性质等,综合性较强,有一定难度.

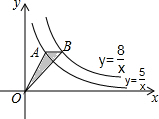 如图,点A在双曲线y=$\frac{5}{x}$上,点B在双曲线y=$\frac{8}{x}$上,且AB∥x轴,则△OAB的面积等于$\frac{3}{2}$.
如图,点A在双曲线y=$\frac{5}{x}$上,点B在双曲线y=$\frac{8}{x}$上,且AB∥x轴,则△OAB的面积等于$\frac{3}{2}$.