题目内容
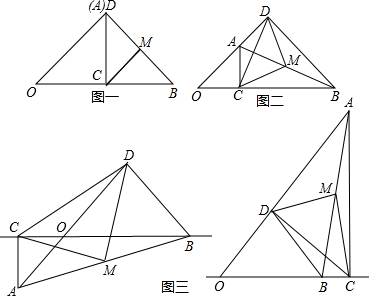
等边△ABC中,D为AB中点,E为BC上一点,以DE为边作等边△DEF,连接CF、AF.
(1)求证:FE=FC;
(2)当∠DAF=90°,CE=1时,求BE的长.
(1)求证:FE=FC;
(2)当∠DAF=90°,CE=1时,求BE的长.
考点:全等三角形的判定与性质,等边三角形的性质
专题:计算题,证明题
分析:(1)根据题意画出图形,借助于等边三角形的性质和圆的定义来解决;
(2)画出图2,过A、D分别作AI⊥BC,DH⊥BC,借助于平行线分线段成比例定理和全等三角形的判定和性质进行分析求解即可.
(2)画出图2,过A、D分别作AI⊥BC,DH⊥BC,借助于平行线分线段成比例定理和全等三角形的判定和性质进行分析求解即可.
解答: (1)证明:如图1,连接CD,
(1)证明:如图1,连接CD,
∵D为AB中点,
∴CD平分∠ACB,∠DCE=
∠ACB=30°,
作FG⊥DE于G,则FG为DE垂直平分线,
∴∠DCE=30°=
∠DFE,
∴F为△CDE外接圆圆心,
∴FE=FC;
(2)解:如图2,
过A、D分别作AI⊥BC,DH⊥BC,其垂足分别为I、H,
∵△ABC为等边三角形,AI⊥BC,
∴AI垂直平分BC,
∴BI=
BC,
∵∠ADF+60°+∠BDE=180°,∠BED+60°+∠BDE=180°,
∴∠ADF=∠BED,
在△ADF和△DEB中,
,
∴△ADF≌△HED(AAS),
∴HE=AD=
AB=
BC,
∵DH⊥BC,AI⊥BC,
∴DH∥AI,
∵△ABI中,D为AB中点,DH∥AI,
∴BH=
BI=
BC,
BC=CE+HE+BH=1+
BC+
BC,
∴BC=4,
∴BE=4-1=3.
 (1)证明:如图1,连接CD,
(1)证明:如图1,连接CD,∵D为AB中点,
∴CD平分∠ACB,∠DCE=
| 1 |
| 2 |
作FG⊥DE于G,则FG为DE垂直平分线,
∴∠DCE=30°=
| 1 |
| 2 |
∴F为△CDE外接圆圆心,
∴FE=FC;
(2)解:如图2,
过A、D分别作AI⊥BC,DH⊥BC,其垂足分别为I、H,
∵△ABC为等边三角形,AI⊥BC,
∴AI垂直平分BC,
∴BI=
| 1 |
| 2 |
∵∠ADF+60°+∠BDE=180°,∠BED+60°+∠BDE=180°,
∴∠ADF=∠BED,
在△ADF和△DEB中,
|
∴△ADF≌△HED(AAS),
∴HE=AD=
| 1 |
| 2 |
| 1 |
| 2 |
∵DH⊥BC,AI⊥BC,
∴DH∥AI,
∵△ABI中,D为AB中点,DH∥AI,
∴BH=
| 1 |
| 2 |
| 1 |
| 4 |
BC=CE+HE+BH=1+
| 1 |
| 2 |
| 1 |
| 4 |
∴BC=4,
∴BE=4-1=3.
点评:该题目考查了等边三角形的性质和全等三角形的判定和性质,作出辅助线是解答的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
在日历上,如果某月的11日是星期四,那么这个月里下面哪个日期是星期五?( )
| A、4日 | B、19日 |
| C、20日 | D、30日 |
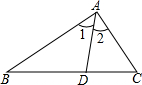 如图,∠1=∠2,∠C=2∠B,求证:AB=AC+CD.
如图,∠1=∠2,∠C=2∠B,求证:AB=AC+CD.