题目内容
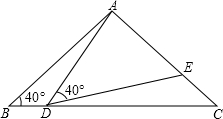 如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.(1)当∠BDA=110°时,∠EDC=
(2)当DC为多少时,△ABD≌△DCE,请说明理由.
考点:全等三角形的判定,等腰三角形的性质
专题:动点型
分析:(1)根据∠BDA=110°以及∠ADE=40°,即可得出∠EDC=180°-∠ADB-∠ADE,进而求出∠DEC的度数;
(2)当DC=2时,利用∠DEC+∠EDC=140°,∠ADB+∠EDC=140°,求出∠ADB=∠DEC,再利用AB=DC=2,即可得出△ABD≌△DCE.
(2)当DC=2时,利用∠DEC+∠EDC=140°,∠ADB+∠EDC=140°,求出∠ADB=∠DEC,再利用AB=DC=2,即可得出△ABD≌△DCE.
解答: 解:(1)∠EDC=180°-∠ADB-∠ADE=180°-110°-40°=30°,
解:(1)∠EDC=180°-∠ADB-∠ADE=180°-110°-40°=30°,
∠DEC=180°-∠EDC-∠C=180°-40°-30°=110°,
故答案是:30;110;
(2)当DC=2时,△ABD≌△DCE,
理由:∵∠C=40°,
∴∠DEC+∠EDC=140°,
又∵∠ADE=40°,
∴∠ADB+∠EDC=140°,
∴∠ADB=∠DEC,
又∵AB=DC=2,
在△ABD和△DCE中
,
∴△ABD≌△DCE(AAS).
 解:(1)∠EDC=180°-∠ADB-∠ADE=180°-110°-40°=30°,
解:(1)∠EDC=180°-∠ADB-∠ADE=180°-110°-40°=30°,∠DEC=180°-∠EDC-∠C=180°-40°-30°=110°,
故答案是:30;110;
(2)当DC=2时,△ABD≌△DCE,
理由:∵∠C=40°,
∴∠DEC+∠EDC=140°,
又∵∠ADE=40°,
∴∠ADB+∠EDC=140°,
∴∠ADB=∠DEC,
又∵AB=DC=2,
在△ABD和△DCE中
|
∴△ABD≌△DCE(AAS).
点评:此题主要考查了等腰三角形的性质以及全等三角形的判定等知识,熟练地应用等腰三角形的性质是解决问题的关键.

练习册系列答案
相关题目
 叙述并证明三角形内角和定理.
叙述并证明三角形内角和定理.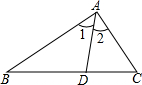 如图,∠1=∠2,∠C=2∠B,求证:AB=AC+CD.
如图,∠1=∠2,∠C=2∠B,求证:AB=AC+CD. 如图,水坝横断面是梯形ABCD,坝顶宽为3m,坝高4m,斜坡AB长5m,斜坡CD的坡度i=1:1.则坝底AD长为
如图,水坝横断面是梯形ABCD,坝顶宽为3m,坝高4m,斜坡AB长5m,斜坡CD的坡度i=1:1.则坝底AD长为