题目内容
10.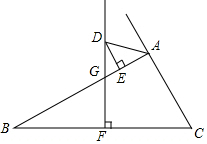 如图所示,在△ABC中,BC边的垂直平分线DF交△BAC的外角平分线AD于点D,F为垂足,DE⊥AB于E,并且AB>AC.求证:BE-AC=AE.
如图所示,在△ABC中,BC边的垂直平分线DF交△BAC的外角平分线AD于点D,F为垂足,DE⊥AB于E,并且AB>AC.求证:BE-AC=AE.
分析 过点D作DG⊥CA交CA的延长线于点G,连接DC,DB,根据垂直平分线和角平分线的性质可先证明Rt△CDG≌Rt△BDE,再证明△ADG≌△ADE,再利用线段的和差可证得结论.
解答  证明:
证明:
如图所示,过点D作DG⊥CA交CA的延长线于点G,连接DC,DB.
∵AD是△ABC的外角平分线,DE⊥AB,DG⊥CA,
∴DE=DG.
∵DF垂直平分BC,
∴DC=DB,
在Rt△CDG与Rt△BDE中
$\left\{\begin{array}{l}{DE=DG}\\{DC=DB}\end{array}\right.$,
∴Rt△CDG≌Rt△BDE(HL),
∴CG=BE.
∵∠GAD=∠EAD,∠AGD=∠AED,AD=AD,
∴在△ADG与△ADE中
$\left\{\begin{array}{l}{∠GAD=∠EAD}\\{∠AGD=∠AED}\\{AD=AD}\end{array}\right.$,
∴△ADG≌△ADE(AAS),
∴AG=AE,
∴CG=AE+AC,
∴BE=AE+AC,
∴BE-AC=AE.
点评 本题主考查了全等三角形的性质和判定、线段的垂直平分线定理和角平分线性质等知识点,添加适当的辅助线,利用中垂线的性质构造三角形全等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19. 如图,在△ABC中,∠CAB=67°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
如图,在△ABC中,∠CAB=67°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
 如图,在△ABC中,∠CAB=67°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
如图,在△ABC中,∠CAB=67°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )| A. | 46° | B. | 50° | C. | 65° | D. | 67° |
20.用代数式表示:“x的5倍与y的和的一半”可以表示为( )
| A. | 5x+$\frac{1}{2}$y | B. | $\frac{1}{2}$(5x+y) | C. | (5x+y)$\frac{1}{2}$ | D. | 5x+y |

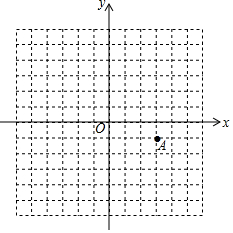 如图,在网格中有点A(3,-1).
如图,在网格中有点A(3,-1).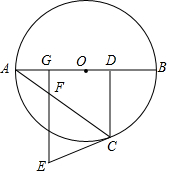 如图,AB是圆O之间,C是圆O上一点,过C作CD⊥AB于D,EC与圆O相切于C且CE=CD.
如图,AB是圆O之间,C是圆O上一点,过C作CD⊥AB于D,EC与圆O相切于C且CE=CD.