题目内容
2.已知命题:“如果两个三角形全等,那么这两个三角形的面积相等”.写出它的逆命题:如果两个三角形的面积相等,那么这两个三角形全等.分析 交换原命题的题设和结论即可得到该命题的逆命题.
解答 解:“如果两个三角形全等,那么这两个三角形的面积相等.”写成它的逆命题:如果两个三角形的面积相等,那么这两个三角形全等.
故答案为:如果两个三角形的面积相等,那么这两个三角形全等;
点评 本题考查逆命题的概念,以及判断真假命题的能力以及全等三角形的判定和性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.若关于x的一元二次方程方程(k-1)x2+4x+1=0有实数根,则k的取值范围是( )
| A. | k<5 | B. | k≥5,且k≠1 | C. | k≤5,且k≠1 | D. | k>5 |
11.在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(9)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:
(1)按表格数据格式,表中的a=123;b=0.404;
(2)请估计:当次数s很大时,摸到白球的频率将会接近0.4;
(3)请推算:摸到红球的概率是0.6(精确到0.1);
(4)试估算:口袋中红球有多少只?
(5)解决了上面4个问题后,请你从统计与概率方面谈一条启示.
| 摸球的次数s | 150 | 300 | 600 | 900 | 1200 | 1500 |
| 摸到白球的频数n | 63 | a | 247 | 365 | 484 | 606 |
| 摸到白球的频率$\frac{n}{s}$ | 0.420 | 0.410 | 0.412 | 0.406 | 0.403 | b |
(2)请估计:当次数s很大时,摸到白球的频率将会接近0.4;
(3)请推算:摸到红球的概率是0.6(精确到0.1);
(4)试估算:口袋中红球有多少只?
(5)解决了上面4个问题后,请你从统计与概率方面谈一条启示.
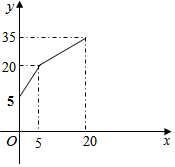 一个水槽有进水管和出水管各一个,进水管每分钟进水m升,出水管每分钟出水n升,水槽在开始5分钟内只进水不出水,随后15分钟内既进水又出水,得到时间x(分)与水量y(升)之间的关系如图所示:
一个水槽有进水管和出水管各一个,进水管每分钟进水m升,出水管每分钟出水n升,水槽在开始5分钟内只进水不出水,随后15分钟内既进水又出水,得到时间x(分)与水量y(升)之间的关系如图所示: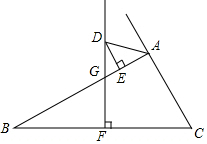 如图所示,在△ABC中,BC边的垂直平分线DF交△BAC的外角平分线AD于点D,F为垂足,DE⊥AB于E,并且AB>AC.求证:BE-AC=AE.
如图所示,在△ABC中,BC边的垂直平分线DF交△BAC的外角平分线AD于点D,F为垂足,DE⊥AB于E,并且AB>AC.求证:BE-AC=AE.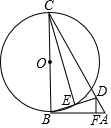 如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作⊙O,交BD于点E,连接CE,过D作DF⊥AB于点F,∠BCD=2∠ABD,求证:
如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作⊙O,交BD于点E,连接CE,过D作DF⊥AB于点F,∠BCD=2∠ABD,求证: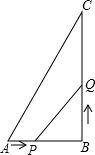 如图,在△ABC中,AB=6cm,BC=12cm,∠B=90°.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,设移动时间为t(s).
如图,在△ABC中,AB=6cm,BC=12cm,∠B=90°.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,设移动时间为t(s).