Question

4．在平面直角坐标系xOy中，直线y=-$\frac{1}{4}$x+n经过点A（-4，2），分别与x，y轴交于点B，C，抛物线y=x²-2mx+m²-n的顶点为D．?
（1）求点B，C的坐标；
（2）①直接写出抛物线顶点D的坐标（用含m的式子表示）；
②若抛物线y=x²-2mx+m²-n与线段BC有公共点，求m的取值范围．?

Answer 1

分析 （1）把A点坐标代入直线解析式，可求得n的值，可得直线解析式，即可求得B、C的坐标；
（2）①把抛物线解析式化为顶点式，结合（1）中所求n的值，可求得D点坐标；②把B、C两点的坐标分别代入抛物线解析式，可求得m的值，从而可求得其取值范围．

解答 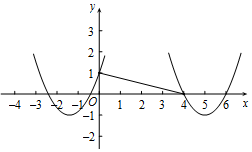解：
（1）把A（-4，2）代入y=$-\frac{1}{4}$x+n中，得n=1，
∴直线解析式为y=$-\frac{1}{4}$x+1，
令y=0可求得x=4，令x=0可得y=1，
∴B（4，0），C（0，1）；
（2）①∵y=x²-2mx+m²-n=（x-m）²-1，
∴D（m，-1）；
②将点（0，1）代入y=x²-2mx+m²-1中，得1=m²-1，解得m=$\sqrt{2}$或m=-$\sqrt{2}$，
将点（4，0）代入y=x²-2mx+m²-1中，得0=16-8m+m²-1，解得m=5或m=3，
∴$-\sqrt{2}≤m≤5$．

点评 本题主要考查二次函数的性质，求得抛物线的解析式是解题的关键，注意数形结合．