题目内容
9. 已知:如图,OA⊥OB,∠BOC=50°,且∠AOD:∠COD=4:7.画出∠BOC的角平分线OE,并求出∠DOE的度数.
已知:如图,OA⊥OB,∠BOC=50°,且∠AOD:∠COD=4:7.画出∠BOC的角平分线OE,并求出∠DOE的度数.
分析 设∠AOD=4x,∠COD=7x,根据题意列出方程即可求得∠COD=140°,然后根据角平分线的定义计算∠COE的度数,最后结合图形计算∠DOE的度数.
解答 解:(1)如右图:
(2)∵OA⊥OB,
∴∠AOB=90°,
∵∠AOD:∠COD=4:7,
∴设∠AOD=4x°,∠COD=7x°,
∵∠AOB+∠AOD+∠COD+∠BOC=360°,且∠BOC=50°,
∴90+7x+4x+50=360,
∴x=20,
∴∠COD=140°.
∵OE是∠BOC的角平分线,
∴$∠COE=\frac{1}{2}\\;∠BOC=25°$∠BOC=25°,
∴∠DOE=∠COD+∠COE=165°,
点评 本题考查的是角的计算,根据题意列出关于x的一元一次方程是解答此题的关键.

练习册系列答案
相关题目
19.下列命题中,真命题有( )
①同旁内角互补;
②三角形的一个外角等于它的两个内角之和;
③一个三角形的最大角不会小于60°,最小角不会大于60°;
④若函数y=(m+1)x${\;}^{{m}^{2}-3}$是正比例函数,且图象在第二、四象限,则m=-2.
①同旁内角互补;
②三角形的一个外角等于它的两个内角之和;
③一个三角形的最大角不会小于60°,最小角不会大于60°;
④若函数y=(m+1)x${\;}^{{m}^{2}-3}$是正比例函数,且图象在第二、四象限,则m=-2.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.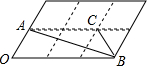 如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点,已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是( )
如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点,已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是( )
 如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点,已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是( )
如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点,已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
17.某农科所在相同条件下做某种作物种子发芽率的试验,结果如表所示:
则该作物种子发芽的概率约为0.910.
| 种子个数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
| 发芽种子个数m | 899 | 1365 | 2245 | 3644 | 7272 | 13680 | 18160 | 27300 |
| 发芽种子频率$\frac{m}{n}$ | 0.899 | 0.910 | 0.898 | 0.911 | 0.909 | 0.912 | 0.908 | 0.910 |
 在平面直角坐标系xOy中,直线y=-$\frac{1}{4}$x+n经过点A(-4,2),分别与x,y轴交于点B,C,抛物线y=x2-2mx+m2-n的顶点为D.?
在平面直角坐标系xOy中,直线y=-$\frac{1}{4}$x+n经过点A(-4,2),分别与x,y轴交于点B,C,抛物线y=x2-2mx+m2-n的顶点为D.? 如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是150米.
如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是150米. 已知:如图,线段a,请按下列步骤画图(用圆规、三角板或量角器画图,不写画法,保留作图痕迹)
已知:如图,线段a,请按下列步骤画图(用圆规、三角板或量角器画图,不写画法,保留作图痕迹)