题目内容
18.半径为2a的圆O中,弦AB的长为$2\sqrt{3}$a,则弦AB所对的圆周角的度数是120°或60°.分析 先根据题意画出图形,连接OA、OB,过O作OF⊥AB,由垂径定理可求出AF的长,根据特殊角的三角函数值可求出∠AOF的度数,由圆周角定理及圆内接四边形的性质即可求出答案.
解答 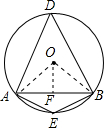 解:如图所示,连接OA、OB,过O作OF⊥AB,则AF=$\frac{1}{2}$AB,∠AOF=$\frac{1}{2}$∠AOB,
解:如图所示,连接OA、OB,过O作OF⊥AB,则AF=$\frac{1}{2}$AB,∠AOF=$\frac{1}{2}$∠AOB,
∵OA=2,AB=2$\sqrt{3}$,
∴AF=$\frac{1}{2}$AB=$\frac{1}{2}$×2$\sqrt{3}$=$\sqrt{3}$,
∴sin∠AOF=$\frac{AF}{OA}$=$\frac{\sqrt{3}}{2}$,
∴∠AOF=60°,
∴∠AOB=2∠AOF=120°,
∴∠ADB=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×120°=60°,
∴∠AEB=180°-60°=120°,
∴∠ADB=180°-120°=60°,
故答案为:120°或60°.
点评 本题考查的是圆周角定理及垂径定理,解答此题时要注意一条弦所对的圆周角有两个,这两个角互为补角.

练习册系列答案
相关题目
 如图,点D、E分别在△ABC的边AB、AC上,∠ADE=∠ACB,求证:∠AED=∠ABC.
如图,点D、E分别在△ABC的边AB、AC上,∠ADE=∠ACB,求证:∠AED=∠ABC.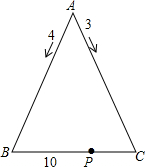 如图,有两只蚂蚁同时从一个等腰三角形的顶点A出发,先分别沿两腰爬行,速度分别为4厘米/秒,3厘米/秒,7秒后在离点B处10厘米的点P相遇,求PC的长.
如图,有两只蚂蚁同时从一个等腰三角形的顶点A出发,先分别沿两腰爬行,速度分别为4厘米/秒,3厘米/秒,7秒后在离点B处10厘米的点P相遇,求PC的长.