题目内容
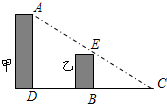 如图,小明站在C处看甲乙两楼楼顶上的点A和点E.C,E,A三点在同一条直线上,点B,E分别在点E,A的正下方且D,B,C三点在同一条直线上.B,C相距20米,D,B相距16米,乙楼高BE为15米,甲楼高AD为(小明身高忽略不计)
如图,小明站在C处看甲乙两楼楼顶上的点A和点E.C,E,A三点在同一条直线上,点B,E分别在点E,A的正下方且D,B,C三点在同一条直线上.B,C相距20米,D,B相距16米,乙楼高BE为15米,甲楼高AD为(小明身高忽略不计)考点:相似三角形的应用
专题:计算题
分析:由题可知,AD和BC平行,所以有相似三角形,根据对应边成比例列式求解即可.
解答:解:∵AD∥BE
∴△CBE∽△CDA,
∴
=
,即
=
,
∴AD=
=27(米),
故答案为:27.
∴△CBE∽△CDA,
∴
| CB |
| CD |
| BE |
| AD |
| 20 |
| 36 |
| 15 |
| AD |
∴AD=
| 36×15 |
| 20 |
故答案为:27.
点评:本题考查相似三角形性质的应用.解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.

练习册系列答案
相关题目
直线AB上的点P到⊙O的圆心O的距离为5,⊙O的直径为10,则直线AB与⊙O的位置关系为( )
| A、相切 | B、相离 |
| C、相交 | D、相交或相切 |
计算(-5)×(-5)的值是( )
| A、25 | B、-25 |
| C、10 | D、-10 |
 如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,
如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,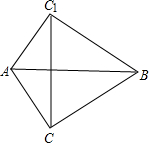 如图,将三边分别为3、4、5的△ABC,沿最长边AB翻转180°成△ABC1,则CC1的长=
如图,将三边分别为3、4、5的△ABC,沿最长边AB翻转180°成△ABC1,则CC1的长= 如图,在△ABC与△ABD中,BC=BD,∠ABC=∠ABD.点E为BC中点,点F为BD中点,连接AE,AF.求证:△ABE≌△ABF.
如图,在△ABC与△ABD中,BC=BD,∠ABC=∠ABD.点E为BC中点,点F为BD中点,连接AE,AF.求证:△ABE≌△ABF.