题目内容
关于x的方程2x2+(m2-9)x+m+1=0,当m= 时,两根互为相反数.
考点:根与系数的关系
专题:计算题
分析:设方程两个为x1,x2,根据根与系数的关系得x1+x2=-
=0,解得m1=3,m2=-3,然后把m的值代入原方程,利用方程的解的情况确定m的值.
| m2-9 |
| 2 |
解答:解:设方程两个为x1,x2,
根据题意得x1+x2=-
=0,解得m1=3,m2=-3,
当m=3时,原方程变形为2x2+4=0,此方程没有实数根,
所以m=-3.
故答案为-3.
根据题意得x1+x2=-
| m2-9 |
| 2 |
当m=3时,原方程变形为2x2+4=0,此方程没有实数根,
所以m=-3.
故答案为-3.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-
,x1•x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
矩形ABCD中,E、F分别为AB、CD中点,如果矩形ABCD与矩形EFCB相似,那么它们的相似比为( )
A、
| ||
B、
| ||
| C、2:1 | ||
| D、1:2 |
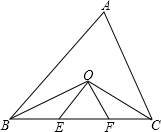 如图,在△ABC中,已知AB=5,BC=6,∠ABC和∠ACB的角平分线BO与CO相交于点O,OE∥AB,OF∥AC,则△OEF的周长为
如图,在△ABC中,已知AB=5,BC=6,∠ABC和∠ACB的角平分线BO与CO相交于点O,OE∥AB,OF∥AC,则△OEF的周长为 如图,AB是半圆O的直径,∠BAC=60°,D是半圆上任意一点,那么∠D的度数是
如图,AB是半圆O的直径,∠BAC=60°,D是半圆上任意一点,那么∠D的度数是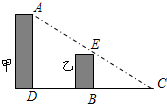 如图,小明站在C处看甲乙两楼楼顶上的点A和点E.C,E,A三点在同一条直线上,点B,E分别在点E,A的正下方且D,B,C三点在同一条直线上.B,C相距20米,D,B相距16米,乙楼高BE为15米,甲楼高AD为(小明身高忽略不计)
如图,小明站在C处看甲乙两楼楼顶上的点A和点E.C,E,A三点在同一条直线上,点B,E分别在点E,A的正下方且D,B,C三点在同一条直线上.B,C相距20米,D,B相距16米,乙楼高BE为15米,甲楼高AD为(小明身高忽略不计)