题目内容
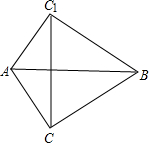 如图,将三边分别为3、4、5的△ABC,沿最长边AB翻转180°成△ABC1,则CC1的长=
如图,将三边分别为3、4、5的△ABC,沿最长边AB翻转180°成△ABC1,则CC1的长=考点:翻折变换(折叠问题)
专题:计算题,几何图形问题
分析:首先设AB与CC1相较于点D,由△ABC的三边分别为3、4、5,且32+42=52,可得△ABC是直角三角形,即可求得CD的长,继而求得答案.
解答: 解:设AB与CC1相较于点D,
解:设AB与CC1相较于点D,
∵△ABC的三边分别为3、4、5,且32+42=52,
∴△ABC是直角三角形,
由折叠的性质可得:AB⊥CD,且CD=C1D,
∴CD=
=
,
∴CC1=2CD=
.
故答案为:
.
 解:设AB与CC1相较于点D,
解:设AB与CC1相较于点D,∵△ABC的三边分别为3、4、5,且32+42=52,
∴△ABC是直角三角形,
由折叠的性质可得:AB⊥CD,且CD=C1D,
∴CD=
| AC•BC |
| AB |
| 12 |
| 5 |
∴CC1=2CD=
| 24 |
| 5 |
故答案为:
| 24 |
| 5 |
点评:此题考查了折叠的性质以及直角三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
到三角形三个顶点的距离相等的点是三角形( )的交点.
| A、三个内角平分线 |
| B、三边垂直平分线 |
| C、三条中线 |
| D、三条高 |
 如图,AB是半圆O的直径,∠BAC=60°,D是半圆上任意一点,那么∠D的度数是
如图,AB是半圆O的直径,∠BAC=60°,D是半圆上任意一点,那么∠D的度数是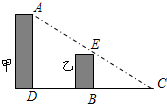 如图,小明站在C处看甲乙两楼楼顶上的点A和点E.C,E,A三点在同一条直线上,点B,E分别在点E,A的正下方且D,B,C三点在同一条直线上.B,C相距20米,D,B相距16米,乙楼高BE为15米,甲楼高AD为(小明身高忽略不计)
如图,小明站在C处看甲乙两楼楼顶上的点A和点E.C,E,A三点在同一条直线上,点B,E分别在点E,A的正下方且D,B,C三点在同一条直线上.B,C相距20米,D,B相距16米,乙楼高BE为15米,甲楼高AD为(小明身高忽略不计)