题目内容
19．
如图，在⊙O中，AB为⊙O的弦，点C为圆上异于A、B的一点，∠OAB=25°，则∠ACB=65°．
分析 根据等腰三角形的性质和三角形内角和定理求出∠AOB的度数，根据圆周角定理计算即可．
解答 解：∵OA=OB，∠OAB=25°，
∴∠AOB=180°-25°-25°=130°，
∴∠ACB=$\frac{1}{2}$∠AOB=65°，
故答案为：65°．
点评 本题考查的是圆周角定理和三角形内角和定理的应用，掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解题的关键．
练习册系列答案
相关题目
9．已知一次函数y=2x+2与x轴y轴分别交于A、B两点，另一直线y=kx+3交x轴正半轴于E、交y轴于F点，如△AOB与E、F、O三点组成的三角形相似，那么k值为（ ）
| A． | -0.5 | B． | -2 | C． | -0.5或-2 | D． | 以上都不对 |
14．将二次函数y=2x2的图象向右平移2个单位，得到该二次函数的表达式是（ ）
| A． | y=2（x+2）2 | B． | y=2（x-2）2 | C． | y=2x2+2 | D． | y=2x2-2 |
11．下列运算正确的是（ ）
| A． | （a+b）2=a2+b2 | B． | $\sqrt{a^2+b^2}$=$\sqrt{a^2}$+$\sqrt{b^2}$ | C． | a2•a3=a5 | D． | $\sqrt{{a}^{4}}$=±a2 |
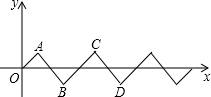如图，在平面直角坐标系中，将斜边长为2个等腰直角三角形按如图所示的位置摆放，得到一条折线O-A-B-C-D…，点P从点O出发沿着折线以每秒$\sqrt{2}$的速度向右运动，2016秒时，点P的坐标是（2016，0）．