题目内容
7.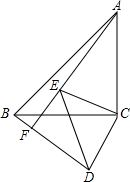 如图,△ABC和△CDE都是等腰直角三角形,AC=BC,DC=EC,∠ACB=∠DCE=90°,AE、BD交于点F,则∠AFB的度数为90°.
如图,△ABC和△CDE都是等腰直角三角形,AC=BC,DC=EC,∠ACB=∠DCE=90°,AE、BD交于点F,则∠AFB的度数为90°.
分析 根据已知条件得到∠ACE=∠BCD,推出△ACE≌△BCD,由全等三角形的性质得到∠CAE=∠CBD,根据三角形的内角和即可得到结论.
解答 解:∵∠ACB=∠DCE=90°,
∴∠ACB-∠BCE=∠DCE-∠BCE,
即∠ACE=∠BCD,
在△ACE与△BCD中,$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{CE=CD}\end{array}\right.$,
∴△ACE≌△BCD,
∴∠CAE=∠CBD,
∵∠CAE+∠BAF+∠ABC=90°,
∴∠DBC+∠CBA+∠BAF=90°,
∴∠AFB=90°.
故答案为:90°.
点评 本题考查了全等三角形的判定和性质,三角形的内角和,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
19. 如图,DC是以AB为直径的半圆上的弦,DM⊥CD交AB于点M,CN⊥CD交AB于点N.AB=10,CD=6.则四边形DMNC的面积( )
如图,DC是以AB为直径的半圆上的弦,DM⊥CD交AB于点M,CN⊥CD交AB于点N.AB=10,CD=6.则四边形DMNC的面积( )
 如图,DC是以AB为直径的半圆上的弦,DM⊥CD交AB于点M,CN⊥CD交AB于点N.AB=10,CD=6.则四边形DMNC的面积( )
如图,DC是以AB为直径的半圆上的弦,DM⊥CD交AB于点M,CN⊥CD交AB于点N.AB=10,CD=6.则四边形DMNC的面积( )| A. | 等于24 | B. | 最小为24 | C. | 等于48 | D. | 最大为48 |
17.已知方程①2x+y=0;②$\frac{1}{2}$x+y=2;③x2-x+1=0;④2x+y-3z=7是二元一次方程的是( )
| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ① |
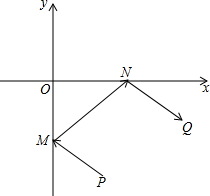 牧马人某天要从马厩牵出马,先到草地边的某一处牧马,再到河边饮水,然后回到帐篷,为了便于研究,以河边为x轴、草地边为y轴建立平面直角坐标系,如图所示,马厩P的坐标为(2,-4),帐篷Q的坐标为(6,-2),请你帮他确定这一天的最短路线.
牧马人某天要从马厩牵出马,先到草地边的某一处牧马,再到河边饮水,然后回到帐篷,为了便于研究,以河边为x轴、草地边为y轴建立平面直角坐标系,如图所示,马厩P的坐标为(2,-4),帐篷Q的坐标为(6,-2),请你帮他确定这一天的最短路线. 如图,在△ABC中,∠ACB=90°,点O是三角形内的一点,且S△OAB=S△OBC=S△OAC,那么$\frac{O{A}^{2}+O{B}^{2}}{O{C}^{2}}$值为5.
如图,在△ABC中,∠ACB=90°,点O是三角形内的一点,且S△OAB=S△OBC=S△OAC,那么$\frac{O{A}^{2}+O{B}^{2}}{O{C}^{2}}$值为5.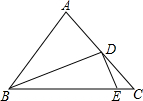 如图,在△ABC中,AB=AC,BD平分∠ABC,DE⊥BD,垂足为D,DE交BC于点E.若DE=5,BD=12,则CD的长为( )
如图,在△ABC中,AB=AC,BD平分∠ABC,DE⊥BD,垂足为D,DE交BC于点E.若DE=5,BD=12,则CD的长为( )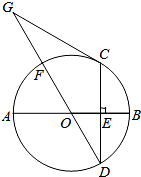 如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°
如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°