题目内容
17.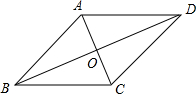 如图,在四边形ABCD中,AB∥DC,对角线AC与BD相交于点O,AO=CO.请你再添一个条件,就能推出四边形ABCD是菱形,则下列条件不符合的是( )
如图,在四边形ABCD中,AB∥DC,对角线AC与BD相交于点O,AO=CO.请你再添一个条件,就能推出四边形ABCD是菱形,则下列条件不符合的是( )| A. | BD平分∠ABC | B. | AB=AD | C. | AC⊥BD | D. | OB=OA |
分析 根据平行线的性质得到∠ABD=∠CDB,根据全等三角形的性质得到AB=CD,于是得到四边形ABCD是平行四边形,根据平行四边形的性质得到AD=BC,根据菱形的判定定理即可得到即可.
解答 解:∵AB∥DC,
∴∠ABD=∠CDB,
在△ABO与△CDO中,$\left\{\begin{array}{l}{∠ABO=∠CDO}\\{∠AOB=∠COD}\\{AO=CO}\end{array}\right.$,
∴△AOB≌△COD,
∴AB=CD,
∴四边形ABCD是平行四边形,
∴AD=BC,
A、∵BD平分∠ABC,
∴∠ABO=∠CBO,
∴∠CBO=∠COD,
∴CB=CD,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形;故A正确;
B、∵AB=AD,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形;故B正确;
C、AC⊥BD,AO=CO,
∴AB=BC,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形;故C正确;
D、∵OB=OA,只能判定四边形是平行四边形,
故选D.
点评 本题考查了菱形的判定,全等三角形的判定与性质,熟练掌握菱形的判定定理是解题的关键,

练习册系列答案
相关题目
5.请思考下列命题的逆命题:①对顶角相等;②角平分线上的点到角两边的距离相等;③到线段两个端点距离相等的点在这条线段的垂直平分线上;④两个全等直角三角形的面积相等,其中逆命题不正确的命题的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9. 为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分:
为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分:
根据以上信息,解答下列问题:
(1)该调查方式是抽样调查;(填“普查”或者“抽样调查”)
(2)本次调查的家庭数为50户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是18%.
(3)若该小区共有1000户家庭,请估计该月用水量不超过9.0吨的家庭数.
 为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分:
为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分:| 分组 | 家庭用水量x/吨 | 家庭数/户 |
| A | 0≤x≤4.0 | 4 |
| B | 4.0<x≤6.5 | 13 |
| C | 6.5<x≤9.0 | |
| D | 9.0<x≤11.5 | |
| E | 11.5<x≤14.0 | 6 |
| F | x>14.0 | 3 |
(1)该调查方式是抽样调查;(填“普查”或者“抽样调查”)
(2)本次调查的家庭数为50户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是18%.
(3)若该小区共有1000户家庭,请估计该月用水量不超过9.0吨的家庭数.
6. 某单位有职工200人,其中青年职工(20-35岁),中年职工(35-50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
某单位有职工200人,其中青年职工(20-35岁),中年职工(35-50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数
表2:小王抽样调查单位10名职工的健康指数
表3:小李抽样调查单位10名职工的健康指数
根据上述材料回答问题:
(1)扇形统计图中老年职工所占部分的圆心角度数为72°
(2)小张、小王和小李三人中,小李的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.
 某单位有职工200人,其中青年职工(20-35岁),中年职工(35-50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
某单位有职工200人,其中青年职工(20-35岁),中年职工(35-50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.表1:小张抽样调查单位3名职工的健康指数
| 年龄 | 26 | 42 | 57 |
| 健康指数 | 97 | 79 | 72 |
| 年龄 | 23 | 25 | 26 | 32 | 33 | 37 | 39 | 42 | 48 | 52 |
| 健康指数 | 93 | 89 | 90 | 83 | 79 | 75 | 80 | 69 | 68 | 60 |
| 年龄 | 22 | 29 | 31 | 36 | 39 | 40 | 43 | 46 | 51 | 55 |
| 健康指数 | 94 | 90 | 88 | 85 | 82 | 78 | 72 | 76 | 62 | 60 |
(1)扇形统计图中老年职工所占部分的圆心角度数为72°
(2)小张、小王和小李三人中,小李的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.
7.3的相反数是( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -3 | D. | 3 |
 如图,E为?ABCD的边AB延长线上的一点,且BE:AB=2:3,连接DE交BC于点F,则CF:AD=3:5.
如图,E为?ABCD的边AB延长线上的一点,且BE:AB=2:3,连接DE交BC于点F,则CF:AD=3:5.