题目内容
17.(1)验证下列各式是否成立:2$\sqrt{\frac{2}{3}}$=$\sqrt{2+\frac{2}{3}}$,3$\sqrt{\frac{3}{8}}$=$\sqrt{3+\frac{3}{8}}$,4$\sqrt{\frac{4}{15}}$=$\sqrt{4+\frac{4}{15}}$,…(2)请你猜测:a$\sqrt{\frac{a}{{a}^{2}-1}}$=$\sqrt{a+\frac{a}{{a}^{2}-1}}$(a>0),并验证你的猜测.
分析 (1)根据二次根式的性质,可得a=$\sqrt{{a}^{2}}$ (a≥0),根据二次根式的乘法:$\sqrt{a}$$•\sqrt{b}$=$\sqrt{a•b}$,可得答案;
(2)根据二次根式的性质,可得a=$\sqrt{{a}^{2}}$ (a≥0),根据二次根式的乘法:$\sqrt{a}$$•\sqrt{b}$=$\sqrt{a•b}$,可得答案.
解答 解:(1)2$\sqrt{\frac{2}{3}}$=$\sqrt{4}$×$\sqrt{\frac{2}{3}}$=$\sqrt{4×\frac{2}{3}}$=$\sqrt{\frac{8}{3}}$=$\sqrt{\frac{6+2}{3}}$=$\sqrt{2+\frac{2}{3}}$,
3$\sqrt{\frac{3}{8}}$=$\sqrt{9}$×$\sqrt{\frac{3}{8}}$=$\sqrt{9×\frac{3}{8}}$=$\sqrt{\frac{27}{8}}$=$\sqrt{\frac{24}{8}+\frac{3}{8}}$=$\sqrt{3+\frac{3}{8}}$,
…
(2)a$\sqrt{\frac{a}{{a}^{2}-1}}$=$\sqrt{a+\frac{a}{{a}^{2}-1}}$,理由如下:
$\sqrt{\frac{a}{{a}^{2}-1}}$=$\sqrt{{a}^{2}}$$•\sqrt{\frac{a}{{a}^{2}-1}}$=$\sqrt{{a}^{2}•\frac{a}{{a}^{2}-1}}$=$\sqrt{\frac{{a}^{3}}{{a}^{2}-1}}$=$\sqrt{\frac{{(a}^{3}-a)+a}{{a}^{2}-1}}$=$\sqrt{\frac{a({a}^{2}-1)+a}{{a}^{2}-1}}$=$\sqrt{a+\frac{a}{{a}^{2}-1}}$.
点评 本题考查了二次根式的性质与化简,利用二次根式的乘法是解题关键.

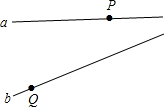 如图所示,直线a,b分别代表公路和河流,点P代表公路a上的公共汽车站,点Q
如图所示,直线a,b分别代表公路和河流,点P代表公路a上的公共汽车站,点Q