题目内容
3.设关于x的方程x2+px+q+1=0的两个实数根是m、n(m<n),关于x的方程x2+px+q-4=0的两个实数根是d、e(d<e),则m、n、d、e的大小关系是( )| A. | m<d<e<n | B. | m<d<n<e | C. | d<m<e<n | D. | d<m<n<e |
分析 由题意得出抛物线y=x2+px+q+1与x轴的两个交点坐标为(m,0),(n,0),把抛物线y=x2+px+q+1向下平移5个单位长度得抛物线y=x2+px+q-4,得出抛物线y=x2+px+q-4与x轴的两个交点坐标为(d,0),(e,0),由图象即可得出结论.
解答 解:∵关于x的方程x2+px+q+1=0的两个实数根是m、n(m<n),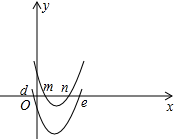
∴抛物线y=x2+px+q+1与x轴的两个交点坐标为(m,0),(n,0),
把抛物线y=x2+px+q+1向下平移5个单位长度得抛物线y=x2+px+q-4,如图所示:
∵关于x的方程x2+px+q-4=0的两个实数根是d、e(d<e),
∴抛物线y=x2+px+q-4与x轴的两个交点坐标为(d,0),(e,0),
根据二次函数的图象得:d<m<n<e;
故选:D.
点评 本题考查了抛物线与x轴的交点、抛物线与一元二次方程的关系;熟记抛物线与x轴的交点坐标与一元二次方程的关系是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.计算(-2ab2)3,结果正确的是( )
| A. | -2a3b6 | B. | -6a3b6 | C. | -8a3b5 | D. | -8a3b6 |
14.点P在第二象限,若该点到x轴的距离为3,到y轴的距离为1,则点P的坐标是( )
| A. | (-1,3) | B. | (-3,1) | C. | (3,-1) | D. | (1,3) |
11.从一幅扑克牌中随机抽取一张牌,它是黑桃的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{5}$ | C. | $\frac{7}{27}$ | D. | $\frac{13}{54}$ |
18.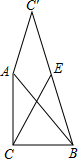 如图,已知△ABC中,∠ACB=90°,AC=BC=2,将直角边AC绕A点逆时针旋转至AC′,连接BC′,E为BC′的中点,连接CE,则CE的最大值为( )
如图,已知△ABC中,∠ACB=90°,AC=BC=2,将直角边AC绕A点逆时针旋转至AC′,连接BC′,E为BC′的中点,连接CE,则CE的最大值为( )
 如图,已知△ABC中,∠ACB=90°,AC=BC=2,将直角边AC绕A点逆时针旋转至AC′,连接BC′,E为BC′的中点,连接CE,则CE的最大值为( )
如图,已知△ABC中,∠ACB=90°,AC=BC=2,将直角边AC绕A点逆时针旋转至AC′,连接BC′,E为BC′的中点,连接CE,则CE的最大值为( )| A. | $\sqrt{5}$ | B. | $\sqrt{2}$+1 | C. | $\frac{\sqrt{2}}{2}$+1 | D. | $\frac{\sqrt{5}}{2}$+1 |
8.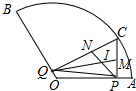 扇形BOA的弧长为$\frac{4}{3}$π,面积为$\frac{4}{3}$π,在$\widehat{AB}$上取一点C,作CP⊥OA于P,CQ⊥OB于Q,△CPO的角平分线PN、QM交于I.当OP≤$\sqrt{3}$时,下列结论中错误的是( )
扇形BOA的弧长为$\frac{4}{3}$π,面积为$\frac{4}{3}$π,在$\widehat{AB}$上取一点C,作CP⊥OA于P,CQ⊥OB于Q,△CPO的角平分线PN、QM交于I.当OP≤$\sqrt{3}$时,下列结论中错误的是( )
 扇形BOA的弧长为$\frac{4}{3}$π,面积为$\frac{4}{3}$π,在$\widehat{AB}$上取一点C,作CP⊥OA于P,CQ⊥OB于Q,△CPO的角平分线PN、QM交于I.当OP≤$\sqrt{3}$时,下列结论中错误的是( )
扇形BOA的弧长为$\frac{4}{3}$π,面积为$\frac{4}{3}$π,在$\widehat{AB}$上取一点C,作CP⊥OA于P,CQ⊥OB于Q,△CPO的角平分线PN、QM交于I.当OP≤$\sqrt{3}$时,下列结论中错误的是( )| A. | ⊙O半径为2 | B. | ∠PCQ=60° | C. | NQ+MP=$\sqrt{3}$ | D. | CN+CM=$\sqrt{3}$ |
15.下列是真命题的是( )
| A. | 过一点有且只有一条直线与已知直线平行 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | $\sqrt{2}$是2的平方根 | |
| D. | 带根号的数是无理数 |
12.半径为30cm,圆心角为120°的扇形恰好围成圆锥的侧面,则这个圆锥的高是( )
| A. | 20$\sqrt{2}$cm | B. | 20$\sqrt{3}$cm | C. | 60$\sqrt{2}$cm | D. | 60$\sqrt{3}$cm |
13.在1,0,π,-3这四个数中,最大的数是( )
| A. | 1 | B. | 0 | C. | π | D. | -3 |