题目内容
8.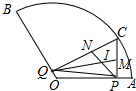 扇形BOA的弧长为$\frac{4}{3}$π,面积为$\frac{4}{3}$π,在$\widehat{AB}$上取一点C,作CP⊥OA于P,CQ⊥OB于Q,△CPO的角平分线PN、QM交于I.当OP≤$\sqrt{3}$时,下列结论中错误的是( )
扇形BOA的弧长为$\frac{4}{3}$π,面积为$\frac{4}{3}$π,在$\widehat{AB}$上取一点C,作CP⊥OA于P,CQ⊥OB于Q,△CPO的角平分线PN、QM交于I.当OP≤$\sqrt{3}$时,下列结论中错误的是( )| A. | ⊙O半径为2 | B. | ∠PCQ=60° | C. | NQ+MP=$\sqrt{3}$ | D. | CN+CM=$\sqrt{3}$ |
分析 首先根据扇形的弧长、面积求出半径、圆心角,不难判断A、B正确,在PQ上取一点R,使得QR=NQ,连接IR,只要证明QN=QR,PM=PR,得NQ+PM=QP,求出QP即可判断C正确,由此即可解决问题.
解答 解:∵扇形BOA的弧长为$\frac{4}{3}$π,面积为$\frac{4}{3}$π,
设扇形的圆心角为n,圆的半径为r,
∴$\frac{nπr}{180}$=$\frac{4}{3}$π,$\frac{nπ{r}^{2}}{360}$=$\frac{4}{3}$π,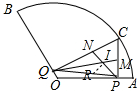
∴nr=240,nr2=480,
∴r=2,n=120°,故A正确.
∵CP⊥OA于P,CQ⊥OB于Q,
∴∠CQO=∠CPO=90°,
∴∠PCQ=360°-(∠CPQ+∠CQO+∠POQ)=60°,故B正确.
在PQ上取一点R,使得QR=NQ,连接IR,
∵△CPO的角平分线PN、QM交于I,
∴∠NQI=∠RQI,∠MPI=∠RPI,
∵QI=QI,
∴△NQI≌△RQI,
∴IN=IR,∠QIN=∠QIR,
∵∠PIQ=180°-$\frac{1}{2}$(∠CQP+∠CPQ)=180°-$\frac{1}{2}$(180°-∠PCQ)=120°,
∴∠QIN=∠QIR=60°,∠PIM=∠PIR=60°,∵IP=IP,
∴△MPI≌△RPI,
∴MP=RP,IM=IR,
∴IN=IR=IM,
∵QR+PR=PQ,
∴NQ+MP=PQ,
∵O、P、C、Q四点共圆,OC为直径,
∴PQ=OC•sin∠PCQ=$\sqrt{3}$,
∴NQ+MP=$\sqrt{3}$,故C正确.
∵OC>PC=MP+CM,OC>QC=NQ+CN,
∴2OC>NQ+MP+CN+CM=$\sqrt{3}$+CN+CM,
∴CN+CM<4-$\sqrt{3}$,
∴CN+CM的值不能确定.故D错误,
故选D.
点评 本题考查扇形的弧长、面积等知识,解题的关键是熟练掌握扇形的弧长公式、面积公式,学会添加常用辅助线,属于中考常考题型.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠B=65°,则∠1的度数是( )
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠B=65°,则∠1的度数是( )| A. | 45° | B. | 25° | C. | 20° | D. | 15° |
| A. | 9 | B. | $\frac{22}{7}$ | C. | π | D. | ($\sqrt{3}$)0 |
| A. | 钟表的指针运动 | B. | 行驶的汽车的车轮 | ||
| C. | 电风扇的转动 | D. | 电梯的升降 |
| A. | m<d<e<n | B. | m<d<n<e | C. | d<m<e<n | D. | d<m<n<e |
(1)在荡秋千的小朋友;
(2)打气筒打气时,活塞的运动;
(3)自行车在行进中车轮的运动;
(4)传送带上,瓶装饮料的移动.
| A. | (1)(2) | B. | (2)(4) | C. | (2)(3) | D. | (1)(3) |
| A. | $\sqrt{2}$+$\sqrt{5}$=$\sqrt{7}$ | B. | 3$\sqrt{5}$-$\sqrt{5}$=2 | C. | $\sqrt{2}×\sqrt{5}$=$\sqrt{10}$ | D. | $\sqrt{18}$÷$\sqrt{3}$=6 |
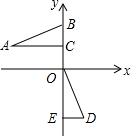 如图,在平面直角坐标系xOy中,点B,C,E在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )
如图,在平面直角坐标系xOy中,点B,C,E在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )| A. | △ABC绕点C顺时针旋转90°,再向下平移3 | |
| B. | △ABC绕点C顺时针旋转90°,再向下平移1 | |
| C. | △ABC绕点C逆时针旋转90°,再向下平移1 | |
| D. | △ABC绕点C逆时针旋转90°,再向下平移3 |