题目内容
12.半径为30cm,圆心角为120°的扇形恰好围成圆锥的侧面,则这个圆锥的高是( )| A. | 20$\sqrt{2}$cm | B. | 20$\sqrt{3}$cm | C. | 60$\sqrt{2}$cm | D. | 60$\sqrt{3}$cm |
分析 设圆锥的底面圆的半径为r,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长和弧长公式得到2πr=$\frac{120•π•30}{180}$,解方程求出r,然后利用扇形的半径等于圆锥的母线长和勾股定理计算圆锥的高.
解答 解:设圆锥的底面圆的半径为r,
根据题意得2πr=$\frac{120•π•30}{180}$,解得r=10,
所以圆锥的高=$\sqrt{3{0}^{2}-1{0}^{2}}$=20$\sqrt{2}$(cm).
故选A.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
相关题目
3.设关于x的方程x2+px+q+1=0的两个实数根是m、n(m<n),关于x的方程x2+px+q-4=0的两个实数根是d、e(d<e),则m、n、d、e的大小关系是( )
| A. | m<d<e<n | B. | m<d<n<e | C. | d<m<e<n | D. | d<m<n<e |
7.-2的相反数是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 0 | D. | -$\frac{1}{2}$ |
17.下列运算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{5}$=$\sqrt{7}$ | B. | 3$\sqrt{5}$-$\sqrt{5}$=2 | C. | $\sqrt{2}×\sqrt{5}$=$\sqrt{10}$ | D. | $\sqrt{18}$÷$\sqrt{3}$=6 |
4.下面是我国几家银行的标志,其中既是轴对称图形,又是中心对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.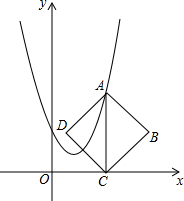 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动,过点A作AC⊥x轴于点C,以AC为对角线作正方形ABCD(点D在AC的左侧),若点D恰好也落在抛物线上,则点A的坐标为( )
如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动,过点A作AC⊥x轴于点C,以AC为对角线作正方形ABCD(点D在AC的左侧),若点D恰好也落在抛物线上,则点A的坐标为( )
 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动,过点A作AC⊥x轴于点C,以AC为对角线作正方形ABCD(点D在AC的左侧),若点D恰好也落在抛物线上,则点A的坐标为( )
如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动,过点A作AC⊥x轴于点C,以AC为对角线作正方形ABCD(点D在AC的左侧),若点D恰好也落在抛物线上,则点A的坐标为( )| A. | (2,2),(3,5) | B. | (2,2),(4,10) | C. | (3,5),(4,10) | D. | (2,2),(4,10),(6,26) |
2.2022年冬奥会由北京和张家口两市联合承办.北京到张家口的自驾距离约为196 000米.196 000用科学记数法表示应为( )
| A. | 1.96×105 | B. | 19.6×104 | C. | 1.96×106 | D. | 0.196×106 |